Dynamic model fixed point
Έστω η αναδρομική σχέση που αναπαριστά ένα δυναμικό μοντέλο:
$$ x_{t+1} &= 3 + 0.4 \, x_t $$
Το σημείο ισορροπίας (fixed point x*) είναι:
$$ x^* &= \frac{3}{1-0.4} = \frac{3}{0.6} = 5 $$
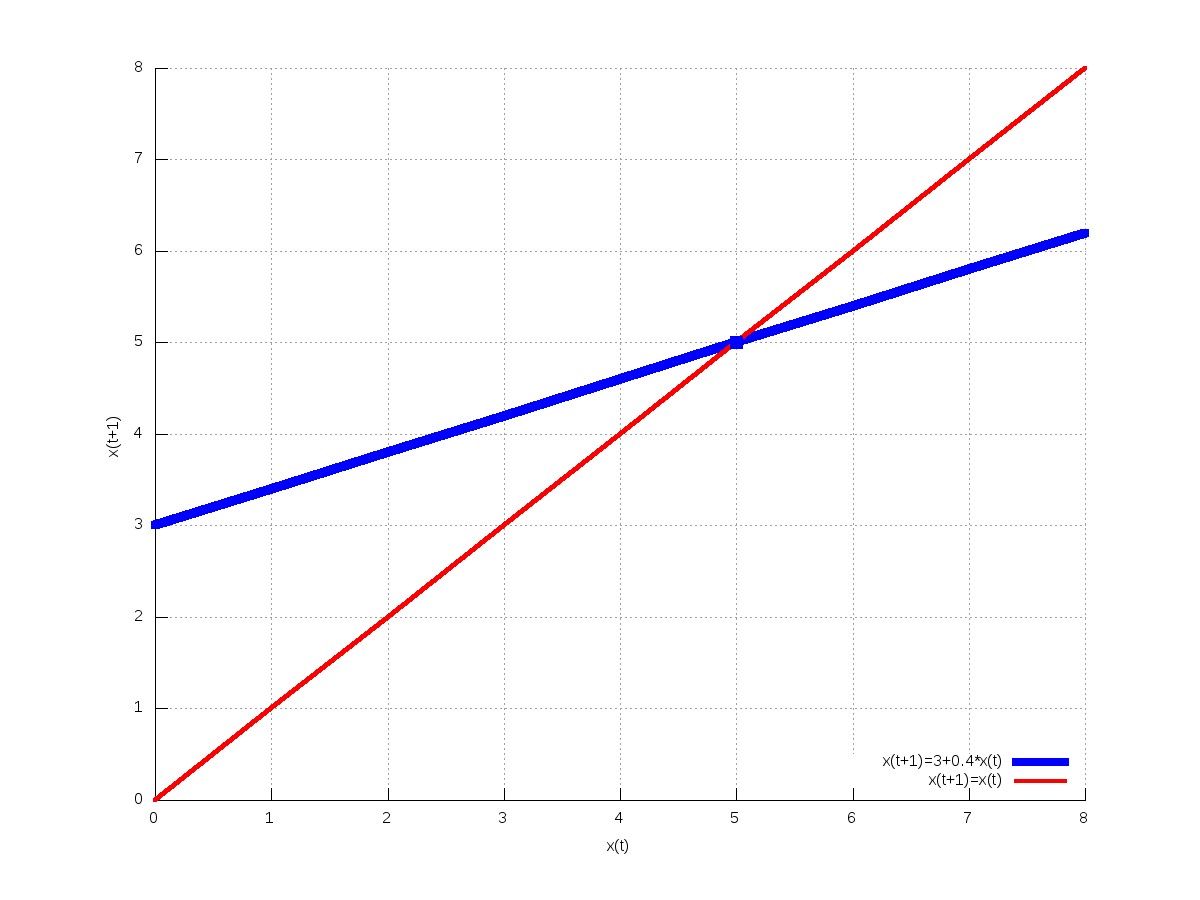
Το γράφημα μπορεί να κατασκευαστεί ως εξής:
clear;
set (gca, 'fontsize', 24)
alpha = 3;
beta = 0.4;
xstar = alpha / (1-beta);
N = 8;
t = 0:N;
x = alpha + beta*t;
plot(t, x, 'b', 'linewidth', 8, t, t, 'r', 'linewidth', 4);
box off;
legend('x(t+1)=3+0.4*x(t)', 'x(t+1)=x(t)', 'Location', 'SouthEast');
xlabel('x(t)');
ylabel('x(t+1)');
grid on;
hold on;
plot(xstar, xstar, 's', 'markersize', 12);
hold off;
print -depsc2 -landscape dynamic1.eps
print -djpg dynamic1.jpg
Έστω dynamic2.m το αρχείο:
clear;
set (gca, 'fontsize', 24)
alpha = 3;
beta = 0.4;
xstar = alpha / (1-beta);
N = 8;
x(1) = 1.5;
for (t = 1:N)
x(t+1) = alpha + beta*x(t);
end
printf ("%4d %f\n", [(0:N)' x']);
Παράδειγμα με x(1) = 1.5:
octave:> dynamic2 ans = 0.00000 1.50000 1.00000 3.60000 2.00000 4.44000 3.00000 4.77600 4.00000 4.91040 5.00000 4.96416 6.00000 4.98566 7.00000 4.99427 8.00000 4.99771
Παράδειγμα με x(1) = 15:
octave:96> dynamic2
ans =
0.00000 15.00000
1.00000 9.00000
2.00000 6.60000
3.00000 5.64000
4.00000 5.25600
5.00000 5.10240
6.00000 5.04096
7.00000 5.01638
8.00000 5.00655
Παρατηρούμε πως και στις δύο περιπτώσεις, είτε με x(1)=1.5,
είτε με x(1)=15, δηλαδή είτε x(1)>x*, είτε x(1)
$$
x_{t+1} = \alpha + \beta \, x_t
$$
με την ευθεία:
$$
x_{t+1} = x_t
$$
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.