Γράφημα της κανονικής κατανομής με την R
Η συνάρτηση πιθανότητας της κανονικής κατανομής είναι:
$$ f(x) = \tfrac{1}{\sqrt{2\pi\sigma^2}}\, e^{-(x-\mu)^2/(2\sigma^2)} $$
Η γραφική παράσταση της τυπικής κανονικής κατανομής (μ=0, σ2=1) μπορεί να γίνει ως:
x <- seq(-4, 4, by=0.04) y <- 1/sqrt(2*pi) * exp(-x^2/2) plot(x, y, type="l", ylab="Πυκνότητα", ylim=c(0,0.45), lwd=2, col="blue")
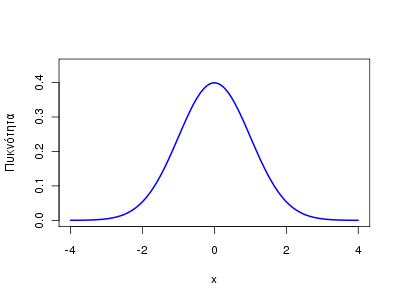
Η πυκνότητα βέβαια μπορεί να βρεθεί και με τη συνάρτηση dnorm:
x <- seq(-4, 4, by=0.04) y <- 1/sqrt(2*pi) * exp(-x^2/2) plot(x, y, type="l", ylab="Πυκνότητα", ylim=c(0,0.45), lwd=2, col="blue")
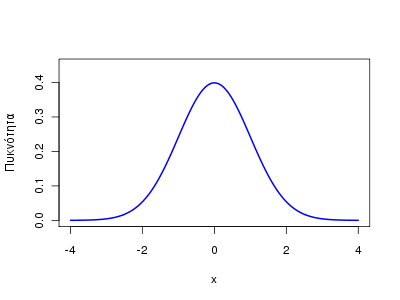
Έτσι, είναι πιο εύκολο να τροποποιηθούν παράμετροι όπως ο μέσος ή η τυπική απόκλιση της κατανομής, πχ;
x <- seq(-4, 4, by=0.04) y <- dnorm(x, mean=0, sd=2) plot(x, y, type="l", ylab="Πυκνότητα", ylim=c(0,0.45), lwd=2, col=4)
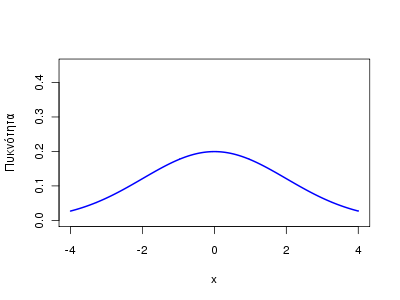
Επίσης, δείτε πως μπορούμε να συγκρίνουμε διάφορα γραφήματα:
x <- seq(-5, 5, by=0.05)
y1 <- dnorm(x, mean=0, sd=1)
y2 <- dnorm(x, mean=0, sd=2)
y3 <- dnorm(x, mean=1, sd=1)
y4 <- dnorm(x, mean=-1, sd=2)
plot(x, y1, type="l", ylab="Πυκνότητα", xlim=c(-5,5), ylim=c(0,0.45), lwd=2, col=1)
lines(x, y2, lwd=2, col=2)
lines(x, y3, lwd=2, col=3)
lines(x, y4, lwd=2, col=4)
legend(-5, 0.45, c("m=0, sd=1","m=0, sd=2", "m=1, sd=1", "m=-1, sd=2"),
col=c(1,2,3,4), lwd=2)
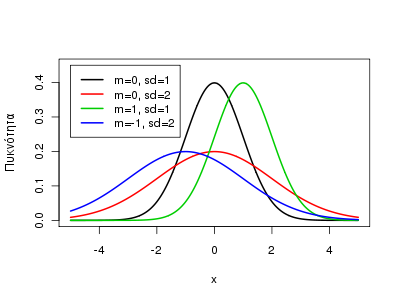
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.