Πλεόνασμα παραγωγού με μη γραμμική συνάρτηση προσφοράς στο Maxima
Έστω η συνάρτηση ζήτησης για ένα προϊόν δίνεται από τη σχέση:
D(q) := -50*q + 140;
Η αντίστοιχη συνάρτηση προσφοράς δίνεται από τη σχέση:
S(q) := 8*q^2 + 28;
Η ισορροπία αγοράς (θετική ρίζα) βρίσκεται στο σημείο:
sol : solve([D(q)=S(q)], q); if rhs(sol[1])>0 then q0:rhs(sol[1]) else q0: rhs(sol[2]); p0 : D(q0);
Γραφικά η ισορροπία παριστάνεται ως:
plot2d([D(q), S(q), p0], [q, 0, 3], [y, 0, 160], [xlabel, "Ποσότητα (q)"], [ylabel, "Τιμή (p)"], [legend, "D", "S", "eq"], [style, [lines, 2, 1], [lines, 2, 2], [lines, 2, 3] ]);
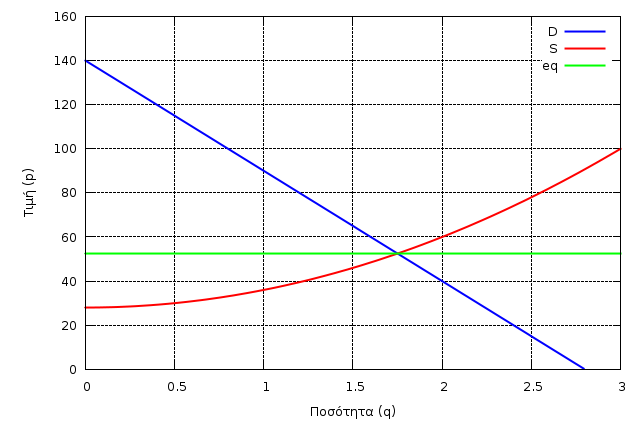
Το πλεόνασμα παραγωγού ορίζεται ως η περιοχή ανάμεσα στην κόκκινη και πράσινη καμπύλη:
PS : q0*p0 - integrate(S(q), q, 0, q0); float(PS);Σημείωση: Οι φράσεις:
ev(q, sol[1]); rhs(sol[1])είναι ισοδύναμες, rhs=right hand side (το δεξί μέρος μιας αλγεβρικής παράστασης)
Επιπλέον εξάσκηση. Έστω πως η καμπύλη ζήτησης περιγράφεται από τη σχέση $$p = 80 -q^2 $$ και η καμπύλη προσφοράς από τη σχέση $$p = 10 + 25q$$. Να υπολογιστεί το πλεόνασμα του καταναλωτή και το συνολικό πλεόνασμα στην ισορροπία της αγοράς.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.