Ολικό, μέσο και οριακό κόστος στο Maxima
Έστω η συνάρτηση κόστους ως προς την ποσότητα (q) του προϊόντος:
$$ TC = q^3 - 10\,q^2 + 60\,q+40 $$
Ορισμός στο Maxima:
TC(q) := q^3 - 10*q^2 + 60*q + 40;
Το μέσο κόστος:
$$ ATC = \frac{TC}{q} $$
Ορισμός στο Maxima:
ATC(q) := ''(TC(q)/q);
Το οριακό κόστος :
$$ MC = \frac{\mathrm{d} TC}{\mathrm{d} q} = TC'(q) $$
Ορισμός στο Maxima:
MC(q) := ''(diff(TC(q),q)) ;
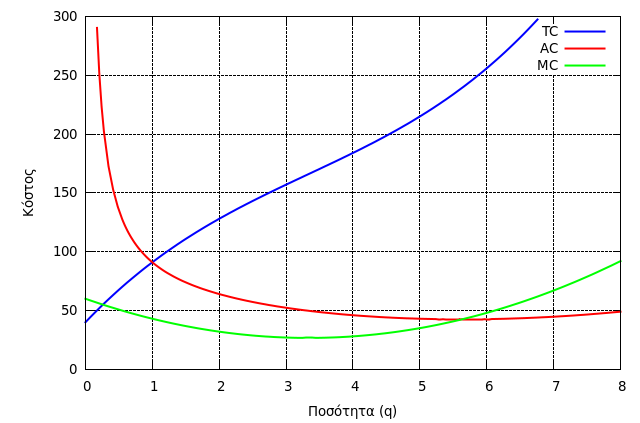
Γραφική αναπαράσταση:
plot2d([TC(q), AΤC(q), MC(q)], [q, 0, 8], [y, 0, 300], [style, [lines,2,1], [lines,2,2], [lines, 2,3]], [xlabel, "Ποσότητα (q)"], [ylabel, "Κόστος"], [legend, "TC", "ATC", "MC"]);
Επιπλέον εξάσκηση: Υπολογίστε τα σημεία τομής των 3 καμπυλών κόστους. Επίσης υπολογίστε το σημείο όπου ελαχιστοποιείται η συνάρτηση μέσου κόστους λύνοντας την εξίσωση
$$ \frac {\mathrm{d} \, AC(q)} {\mathrm{d} \, q} = 0 $$
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.