Μεγιστοποίηση κέρδους με γνωστή συνάρτηση κέρδους στο Maxima
Έστω πως τα κέρδη μιας επιχείρησης περιγράφονται από τη συνάρτηση:
$$ \pi = 800q - 4 q^2 $$
όπου q η παραγόμενη ποσότητα.
Για να υπολογίσουμε την ποσότητα (q) στην οποία μεγιστοποιούνται τα κέρδη θα εργαστούμε ως εξής:
- Ορισμός της συνάρτησης κέρδους:
P(q) := 800*q-4*q^2;
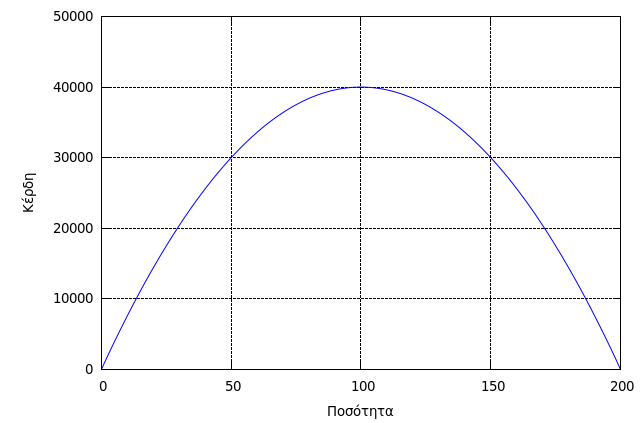
- Το γράφημα της συνάρτησης κέρδους (προαιρετικά):
plot2d([P(q)], [q,0,200], [y,0,50000], [xlabel, "Ποσότητα"], [ylabel, "Κέρδη"]);
- Ορισμός της πρώτης παραγώγου:
g1(q) := ''( diff(P(q), q, 1) );
- Επίλυση της εξίσωσης
$$d\pi / dq = 0$$
και υπολογισμός της ποσότητας που μεγιστοποιεί τα κέρδη:sol : solve(g1(q)=0, q); q0 : rhs(sol[1]);
- Το μέγιστο κέρδος είναι:
P(q0);
- Το ακρότατο είναι μέγιστο, επιβεβαίωση με τη συνθήκη δεύτερης τάξης
(αρνητικός αριθμός στην τιμή q=q0):
g2(q) := ''( diff(P(q), q, 2) ); g2(q0);
Επιπλέον εξάσκηση:
Να βρείτε το σημείο μεγιστοποίησης $$q_0$$ κέρδους όταν το κέρδος περιγράφεται από
τη σχέση
$$
\pi = 1000\,q-4\,{q}^{5/2}
$$
Να υπολογίσετε την κλίση της καμπύλης κέρδους στα σημεία $$q_0-1$$
και $$q_0+1$$.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.