Καμπύλη ζήτησης με παλινδρόμηση στην R
Ας υποθέσουμε πως για τη ζήτηση ενός προϊόντος έχουμς τον ακόλουθο πίνακα τιμών:
| Ποσότητα (q) | Τιμή (p) |
|---|---|
| 2 | 120 |
| 6 | 100 |
| 8 | 85 |
| 10 | 55 |
| 15 | 30 |
Μπορούμε να παραστήσουμε τα παραπάνω δεδομένα σε διάγραμμα διασποράς με γραμμή που ενώνει τα σημεία:
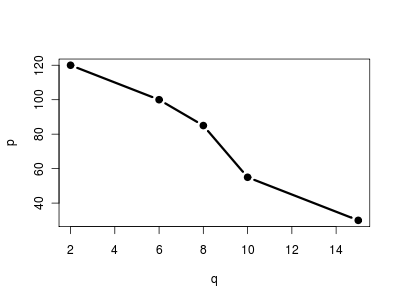
με την εντολή:
> plot(q, p, pch=19, type="b", lwd=3)
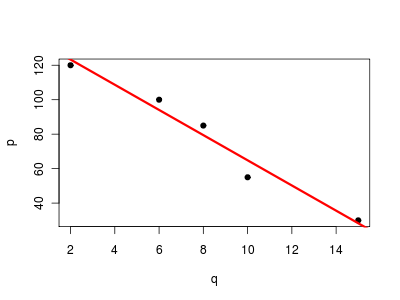
Θα εκτιμήσουμε ζήτησης από το γραμμικό μοντέλο:
$$ p = \beta_0 + \beta_1 q + u $$
ως εξής:
> lm(p ~ q)
Call:
lm(formula = p ~ q)
Coefficients:
(Intercept) q
137.9 -7.3
Ή, περισσότερο αναλυτικά:
> D <- lm(p ~ q)
> summary(D)
Call:
lm(formula = p ~ q)
Residuals:
1 2 3 4 5
-3.30 5.93 5.54 -9.85 1.68
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 137.909 7.376 18.70 0.00033
q -7.306 0.796 -9.18 0.00274
Residual standard error: 7.67 on 3 degrees of freedom
Multiple R-squared: 0.966, Adjusted R-squared: 0.954
F-statistic: 84.2 on 1 and 3 DF, p-value: 0.00274
Αυτό σημαίνει πως η ζήτηση περιγράφεται από τη σχέση:
$$ p = 137.9 - 7.3 q $$
Σημείωση:
Από μεθοδολογική άποψη είναι σαφώς ορθότερο να εκτιμηθεί μια σχέση
$$
q = f(p)
$$
δηλαδή η συνάρτηση ζήτησης και όχι η καμπύλη ζήτησης.
Για το σκοπό της επίδειξης της συνάρτησης lm το παραπάνω παράδειγμα είναι
πιστεύω περισσότερο κατανοητό σε πρωτοετείς φοιτητές.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.