Υπολογισμός μέσω ρυθμού ανάπτυξης ΑΕΠ στο Maxima
Ας υποθέσουμε πως το ΑΕΠ μιας οικονομίας αυξήθηκε από 5.5 σε 14.3 μέσα σε 40 χρόνια. Ποιος είναι ο μέσος ρυθμός αύξησης; Σημείωση: Η μονάδα μέτρησης του ΑΕΠ (πχ δισ. €) δε έχει σημασία, αρκεί να είναι η ίδια και στις δύο μετρήσεις.
Σε καμία περίπτωση δεν είναι: $$ \frac{14.3-5.5}{40} $$
Ο μέσος ρυθμός μεταβολής, δίνεται από τη λύση της εξίσωσης:
$$ (1+a)^{40} = \frac{GDP_2}{GDP_1} $$
Για πρακτικούς λόγους, είναι πολύ καλύτερο να λύσετε τη εξίσωση μετά από λογαρίθμηση:
$$ \log\left( (1+a)^{40}\right) = \log\left( \frac{GDP_2}{GDP_1} \right) $$
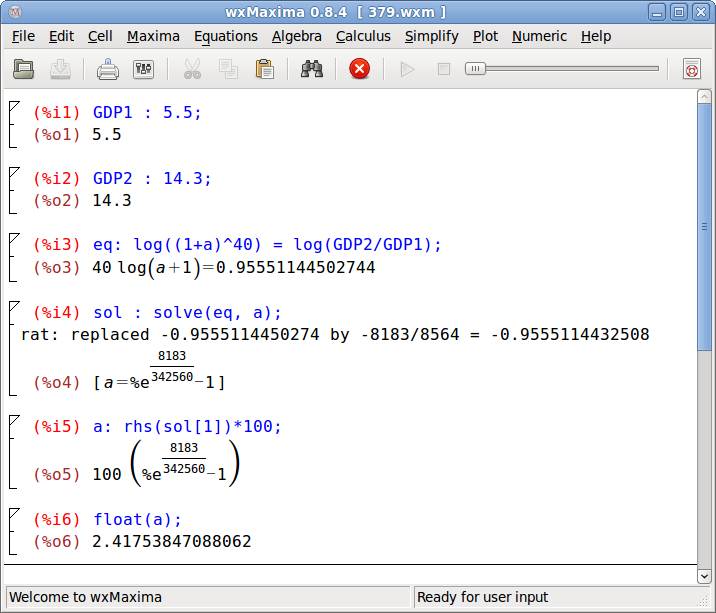
Το πρόβλημα μπορεί να λυθεί στο maxima ως εξής:
GDP1 : 5.5; GDP2 : 14.3; eq : log((1+a)^40) = log(GDP2/GDP1); sol : solve(eq, a); a : rhs(sol[1])*100; float(a);
Οι δύο τελευταίες εντολές είναι για την περίπτωση που θέλουμε το ρυθμό μεταβολής εκφρασμένο ως αριθμητικό ποσοστό επί τοις εκατό.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.