Υπολογισμός ακρότατου συνάρτησης με παραγώγους στο Maxima
Έστω η συνάρτηση:
$$f\left( x\right) = \frac{4}{{x}^{2} -2 \,x+4}$$
Να βρεθούν τα ακρότατα (ελάχιστα ή μέγιστα).
Λύση:
- Εισαγωγή της συνάρτησης:
f(x) := 4/(x^2-2*x+4);
$$f\left( x\right) :=\frac{4}{{x}^{2}+\left( -2\right) \,x+4}$$ - Η πρώτη παράγωγος:
g(x) := ''(diff(f(x), x));
$$g\left( x\right) =-\frac{4\,\left( 2\,x-2\right) }{{\left( {x}^{2}-2\,x+4\right) }^{2}}$$ - Μηδενίζεται στο σημείο:
sol: solve(g(x)=0); x0 : rhs(sol[1]);
$$x0 = 1$$ - Επομένως η συνάρτηση έχει ακρότατο στο σημείο $$x_0=1$$,
η δεύτερη παράγωγος στο σημείο αυτό είναι:
g2(x) := ''(diff(f(x), x, 2));
$$g2\left( x\right) = \frac{8\,{\left( 2\,x-2\right) }^{2}}{{\left( {x}^{2}-2\,x+4\right) }^{3}}-\frac{8}{{\left( {x}^{2}-2\,x+4\right) }^{2}}$$g2(x0);
$$-\frac{8}{9}$$ - αρνητική, επομένως το στο σημείο x=1 η f(x) έχει μέγιστο
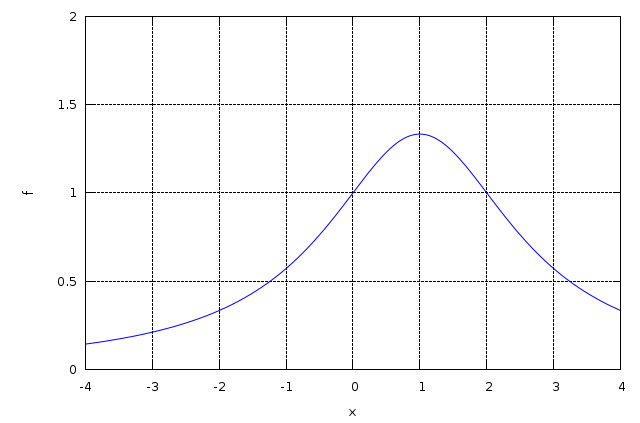
Δείτε και το γράφημα της f(x):
Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.