Το υπόδειγμα Solow οικονομικής μεγέθυνσης με το Octave/Matlab
Για τις λεπτομέρειες του υποδείγματος Solow θα χρειαστεί να συμβουλευτείτε κάποιο βιβλίο μακροοικονομικής.
- Y, το προϊόν
- K, το κεφάλαιο
- N, το εργατικό δυναμικό
- A, το επίπεδο τεχνολογίας
- s, ο λόγος (ποσοστό) της αποταμίευσης
- δ, ο λόγος (ποσοστό) απόσβεσης
η συνάρτηση παραγωγής :
$$ Y_t = A K_t^{1-\alpha} N^{\alpha} $$
παραγωγή = κατανάλωση + αποταμίευση:
$$ Y_t = C_t + I_t $$
αποταμίευση ως ποσοστού της παραγωγής:
$$ I_t = s Y_t $$
μεταβολή του κεφαλαίου:
$$ K_{t+1} = (1-\delta) K_t + I_t $$
επομένως:
$$ K_{t+1} = s A K_t^{1-\alpha} N^{\alpha} + (1-\delta) K_t^{1-\alpha} N^{\alpha} $$
Άσκηση 1: Υποθέτοντας κάποιες τιμές στις παραμέτρους του προβλήματος (δείχνονται παρακάτω μέσα στο πρόγραμμα) και αρχική τιμή του κεφαλαίου $$K_1 = 10$$ να υπολογίζεται την εξέλιξη του κεφαλαίου για 50 περιόδους. Να κάνετε το διάγραμμα Κεφαλαίου ως προς το χρόνο (τοποθετήστε επίσης και την ευθεία K=Kmax). Τι παρατηρείτε;
clear;
T = 50;
A = 1;
N = 10;
alpha = 2/3;
s = 0.2;
delta = 0.1;
K(1) = 10;
for (t = 2:T)
K(t) = s*A*K(t-1)^(1-alpha)*N^alpha + (1-delta)*K(t-1);
end
Time = 1:T;
Kc(1:T) = K(T);
plot(Time, Kc, 'r', "linewidth", 2, K, 'b', "linewidth", 2)
xlabel('Time');
ylabel('Capital');
grid on;
legend({'K at t=50','K evolution'}, 'Location', 'SouthEast');
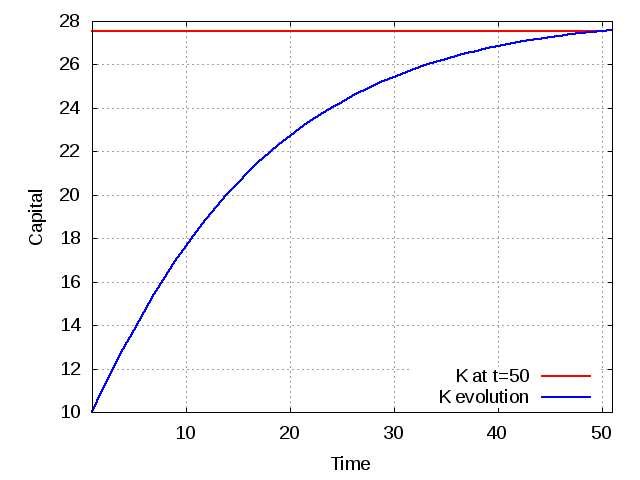
Άσκηση 2: Υποθέτοντας τις ίδιες τιμές στις παραμέτρους του προβλήματος όπως και πριν (δείχνονται παρακάτω μέσα στο πρόγραμμα) να υπολογίζεται την εξέλιξη του κεφαλαίου μέχρις ότου η μεταβολή γίνει μικρότερη από 0.0001, δηλαδή επέλθει σταθεροποίηση σε ποσοστό 0.1 τοις χιλίοις. Να κάνετε το διάγραμμα Κεφαλαίου ως προς το χρόνο (τοποθετήστε επίσης και την ευθεία K=Kmax). Τι παρατηρείτε;
clear;
A = 1;
N = 10;
alpha = 2/3;
s = 0.2;
delta = 0.1;
K(1) = 10;
eps = 1e-4;
t = 1;
do
++t;
K(t) = s*A*K(t-1)^(1-alpha)*N^alpha + (1-delta)*K(t-1);
until ( abs(K(t)-K(t-1)) < eps )
T = length(K);
Time = 1:T;
Kc(1:T) = K(T);
plot(Time, Kc, 'r', "linewidth", 2, K, 'b', "linewidth", 2)
xlabel('Time');
ylabel('Capital');
grid on;
legend({'Kc at t=T','K evolution'}, 'Location', 'SouthEast');
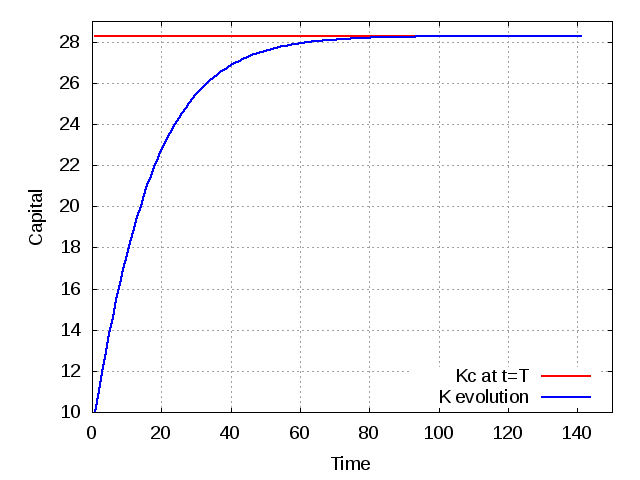
Άσκηση 3: Σε κατάσταση σταθερής κατάστασης το κεφάλαιο είναι (αναλυτική λύση):
$$ K = N \, \left( \frac{sA}{\delta} \right) ^ {1/\alpha} $$
Να πάρετε τις τιμές K(50) και K(T) από την τελευταία υπολογιστική λύση και να βρείτε το ποσοστιαίο σφάλμα της μεθόδου στις δύο περιπτώσεις. Πόσο καλά προσεγγίζει η υπολογιστική την αναλυτική λύση;
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.