Επίλυση μη γραμμικής εξίσωσης με το Octave
Έστω η εξίσωση:
$$3\,{x}^{3}-x-1 = 0$$
Η οποία έχει ρίζα:
$$x = \frac{{\left( \sqrt{77}+9\right) }^{\frac{2}{3}}+{2}^{\frac{2}{3}}}{3\,{2}^{\frac{1}{3}}\,{\left( \sqrt{77}+9\right) }^{\frac{1}{3}}}$$
ή, προσεγγιστικά: $$ x = 0.851383 $$
Για να λύσουμε μια μη γραμμική εξίσωση στο Octave θα χρειαστεί να γράψουμε την αντίστοιχη συνάρτηση και να καλέσουμε τη ρουτίνα fsolve:
clear;
function y=f(x)
y = 3*x.^3 - x - 1;
end
x0 = 2;
fsolve("f", x0)
Η τελευταία εντολή θα δώσει τη λύση, πχ:
octave:> fsolve("f", x0)
ans = 0.85138
Ή, με περισσότερα δεκαδικά ψηφία:
octave:> format long
octave:> fsolve("f", x0)
ans = 0.851383078787220
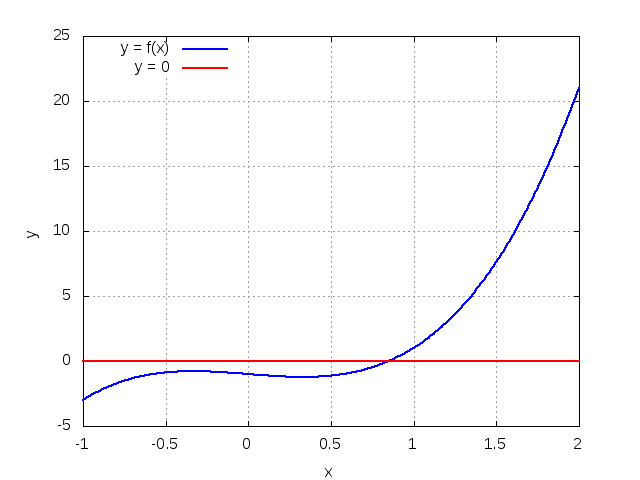
Η λύση μπορεί να επιβεβαιωθεί και γραφικά:
x = [-1 : 0.01 : 2]';
y0 = zeros(length(x), 1)';
y = f(x);
plot(x, y, 'b', 'linewidth', 2, x, y0, 'r', 'linewidth', 2);
xlabel('x');
ylabel('y');
legend({'y = f(x)', 'y = 0'}, 'Location', 'NorthWest');
grid on;
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.