Υπολογισμός της απώλειας κοινωνικής ευημερίας με το Maxima
Ακολουθεί ένα παράδειγμα υπολογισμού της απώλειας κοινωνικής ευημερίας (Deadweight Loss) μετά την επιβολή φόρου.
Υποθέτουμε πως η ζήτηση ενός προϊόντος περιγράφεται από τη σχέση:
$$ p = 50 - 5q $$
Ενώ η προσφορά προϊόντος περιγράφεται από τη σχέση:
$$ p = 10 + 5q $$
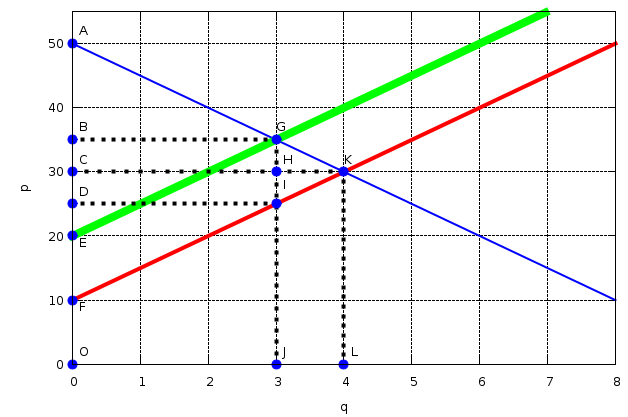
Η κυβέρνηση επιβάλει φόρο ίσο με 10 χρηματικές μονάδες ανά μονάδα προϊόντος. Η καμπύλη προσφοράς μεταβάλλεται. Να υπολογιστεί η απώλεια κοινωνικής ευημερίας, η οποία αντιστοιχεί στο εμβαδόν της επιφάνειας GIK του παρακάτω σχήματος.
Σταδιακή λύση του προβλήματος
-
Ορίζουμε τις καμπύλες ζήτησης και προσφοράς (τιμή ως προς την ποσότητα)
πριν τη φορολογία:
D(q) := 50 - 5*q; S0(q) := 10 + 5*q;
-
Ορίζουμε τη καμπύλη προσφοράς μετά τη φορολογία:
tax : 10; S1(q) := S0(q) + tax;
-
Βρίσκουμε την ποσότητα ισορροπίας πριν το φόρο (σημείο L):
sol : solve(D(q)=S0(q), q); q0 : rhs(sol[1]);
-
Βρίσκουμε την ποσότητα ισορροπίας μετά το φόρο (σημείο J):
sol : solve(D(q)=S1(q), q); q1 : rhs(sol[1]);
-
Υπολογισμός της απώλειας κοινωνικής ευημερίας ως εμβαδού τριγώνου (GIK):
DWL : (1/2) * tax * (q0-q1);
-
Υπολογισμός της απώλειας κοινωνικής ευημερίας με ολοκλήρωση:
DWL : integrate(D(q), q, q1, q0) - integrate(S0(q), q, q1, q0);
Υπολογίζουμε το εμβαδό με τον τύπο ορθογωνίου τριγώνου με την παραδοχή πως η βάση αντιστοιχεί στον κάθετο άξονα (GI=BD=EF) και το ύψος η διαφορά στον οριζόντιο άξονα (ΗΚ=JL).
Περισσότερη εξάσκηση
- Υπολογίστε την ελαστικότητα στα σημεία ισορροπίας
- Υπολογίστε την ποσότητα DWL αν η καμπύλη ζήτησης περιγράφεται από τη σχέση p = 50-10q και συγκρίνετε το αποτέλεσμα
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.