Επίλυση διαφορικής εξίσωσης με το Maxima
Οι διαφορικές εξισώσεις (1ης τάξης) έχουν τη μορφή:
$$ \frac{dy}{dx} = f(x,y) $$
Λύση της διαφορικής εξίσωσης είναι μια συνάρτηση
$$ y = y(x) $$
για την οποία ισχύει:
$$ \frac{d}{dx} \, y(x) = f(x, y(x)) $$
Παράδειγμα
Έστω η εξίσωση
$$ \frac{dy}{dx} = \frac{x+y}{2} $$
η λύση είναι:
$$ y = c\,{e}^{\frac{x}{2}}-x-2 $$
Ο υπολογισμός της σταθεράς c γίνεται αν είναι γνωστές οι αρχικές συνθήκες της εξίσωσης. Για παράδειγμα αν x=0, y=1, τότε c=3
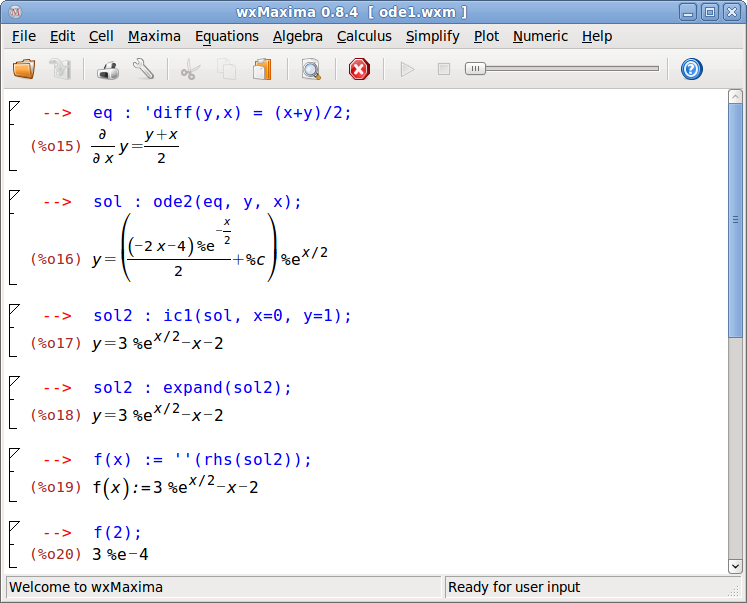
Η διαδικασία επίλυσης μιας διαφορικής εξίσωσης στο Maxima έχει ως εξής:
eq : 'diff(y,x) = (x+y)/2; sol : ode2(eq, y, x); sol2 : ic1(sol, x=0, y=1); sol2 : expand(sol2); f(x) := ''(rhs(sol2));
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.