Η μέθοδος Euler για την επίλυση διαφορικής εξίσωσης με το Excel/Calc
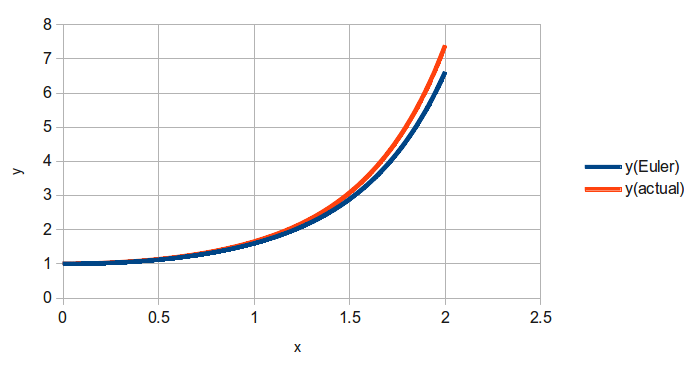
Έστω η διαφορική εξίσωση:
με αρχικές συνθήκες
Η αναλυτική λύση της εξίσωσης είναι:
ή:
Η μέθοδος Euler είναι μι προσεγγιστική αριθμητική μέθοδος για τον υπολογισμό του πίνακα τιμών x,y. Βασίζεται στα εξής βήματα:
- Γράφουμε την διαφορική εξίσωση στη μορφή
για παράδειγμα:
όπου:
- Επιλέγουμε το βήμα αύξησης
για παράδειγμα:
- Υπολογίζουμε τους όρους της ακολουθίας με βάση τους αναδρομικούς τύπους:
για:
Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.