Η μέθοδος lsode για την επίλυση διαφορικών εξισώσεων με το Octave
Έστω η διαφορική εξίσωση:
$$ \frac{dy}{dx} = xy $$
με αρχικές συνθήκες
$$ x_0 = 0, \quad y_0 =1 $$
Να πως υπολογίζονται οι τιμές στο πεδίο [0,2] με βήμα, πχ,
function xdot = f(x,t)
xdot = x*t;
end
x0 = 1;
t = linspace (0, 2, 101)';
x = lsode ("f", x0, t);
Το γράφημα των τιμών, μαζί τις αντίστοιχες τιμές της αναλυτικής λύσης φαίνεται παρακάτω.
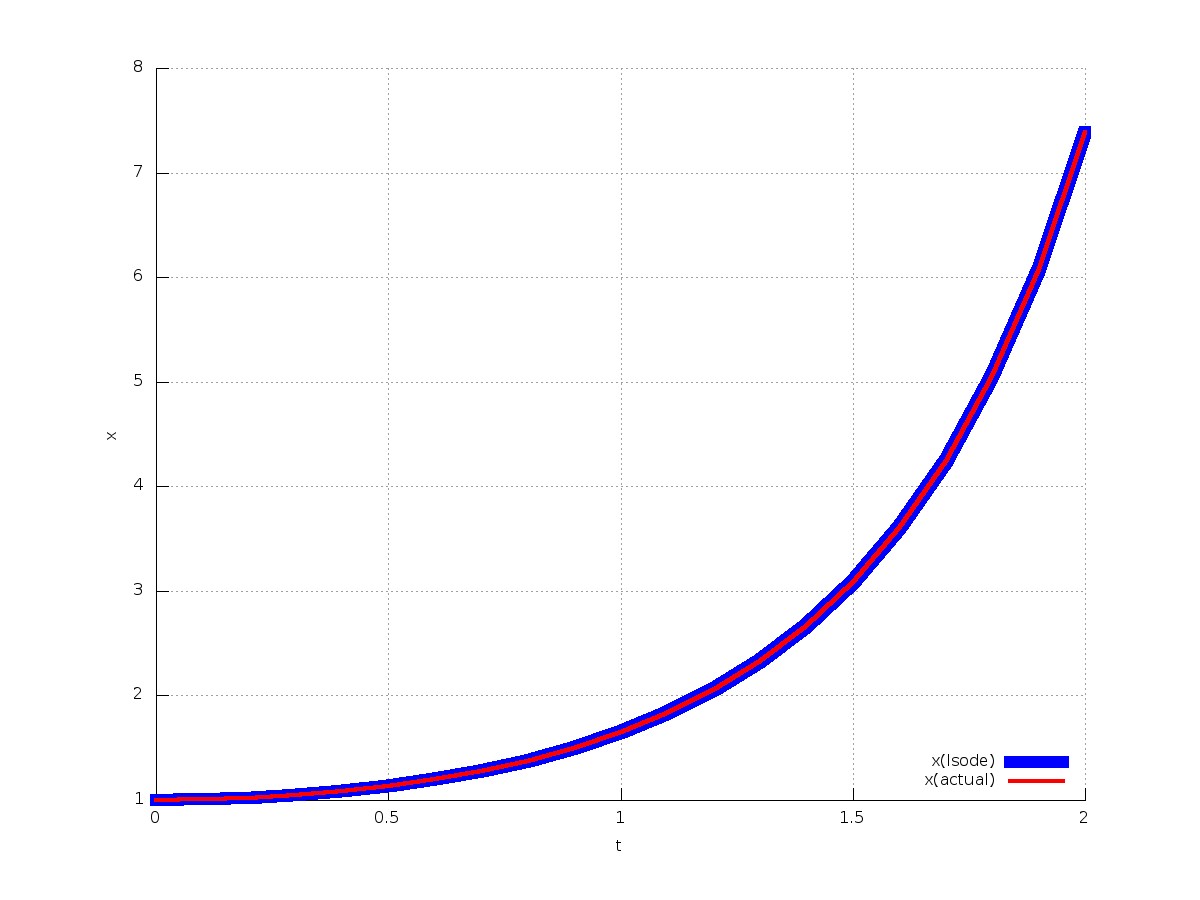
Το γράφημα μπορεί να κατασκευαστεί ως εξής:
clear;
set (gca, 'fontsize', 24)
function xdot = f(x,t)
xdot = x*t;
end
x0 = 1;
t = linspace (0, 2, 21)';
x = lsode ("f", x0, t);
x1 = exp(t.^2 / 2);
plot(t, x, 'b', 'LineWidth', 12, t, x1, 'r', 'LineWidth', 4);
box off;
grid on;
xlabel('t');
ylabel('x');
legend('x(lsode)', 'x(actual)', 'Location', 'SouthEast');
print -depsc2 -landscape lsode1.eps
print -djpg lsode1.jpg
Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.