Επίλυση συστήματος διαφορικών εξισώσεων με το Maxima
Έστω το σύστημα διαφορικών εξισώσεων:
$$ \begin{array}{l l} \dot{x} & = -y+2\,{x}^{2}+t \\ \dot{y} &= \[-{y}^{2}+x-1 \\ \end{array} $$
Η λύση του είναι;
$$ \begin{array}{l l} \mathrm{x}\left( t\right) &= -t\,y+2\,t\,{x}^{2}+\frac{{t}^{2}}{2}+\mathrm{x}\left( 0\right) \\ \mathrm{y}\left( t\right) &= -t\,{y}^{2}+t\,x-t+\mathrm{y}\left( 0\right) \\ \end{array} $$
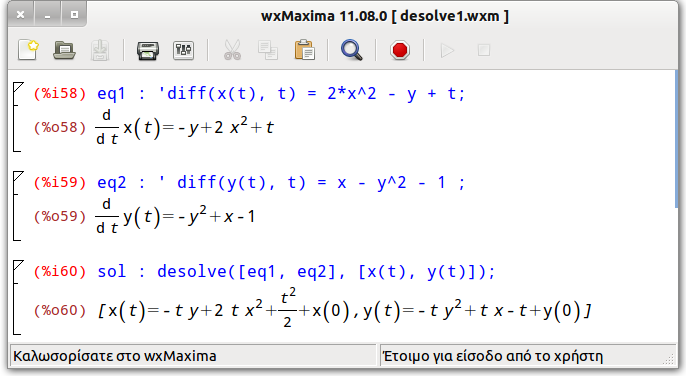
Στο maxima ο υπολογισμός της (γενικής) λύσης γράφετε ως εξής:
eq1 : 'diff(x(t), t) = 2*x^2 - y + t; eq2 : 'diff(y(t), t) = x - y^2 - 1; sol : desolve([eq1, eq2], [x(t), y(t)]);
Αν είναι γνωστές οι αρχικές συνθήκες, τότε η ειδική λύση μπορεί να βρεθεί ως:
eq1 : 'diff(x(t), t) = 2*x^2 - y + t; eq2 : 'diff(y(t), t) = x - y^2 - 1; atvalue(x(t), t=0, 1); atvalue(y(t), t=0, -1); sol : desolve([eq1, eq2], [x(t), y(t)]);Δηλώνοντας αντίστοιχα τις τιμές t0,x0 και t0,y0.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.