Επίλυση συστήματος διαφορικών εξισώσεων με το Octave/Matlab
Έστω το σύστημα διαφορικών εξισώσεων:
$$ \begin{array}{l l} \dot{x_1} & = -x_2+2\,{x_1}^{2} + t \\ \dot{x_2} &= \[-{x_2}^{2}+x_1 - 1 \\ \end{array} $$
Η λύση του είναι;
$$ \begin{array}{l l} \mathrm{x_1}\left( t\right) &= -t\,x_2+2\,t\,{x_1}^{2}+\frac{{t}^{2}}{2}+\mathrm{x_1}\left( 0\right) \\ \mathrm{x_2}\left( t\right) &= -t\,{x_2}^{2}+t\,x-t+\mathrm{x_2}\left( 0\right) \\ \end{array} $$
Έστω πως οι αρχικές συνθήκες είναι x1(0)=1, x2(0)=1. Στο Octave ο υπολογισμός της λύσης γράφετε ως εξής:
function xdot = f(x,t)
xdot(1) = 2*x(1) - x(2) + t;
xdot(2) = x(1) - x(2)^2 - 1;
end
x0 = [1, 1]';
t = linspace(0, 1, 501);
x = lsode('f', x0, t);
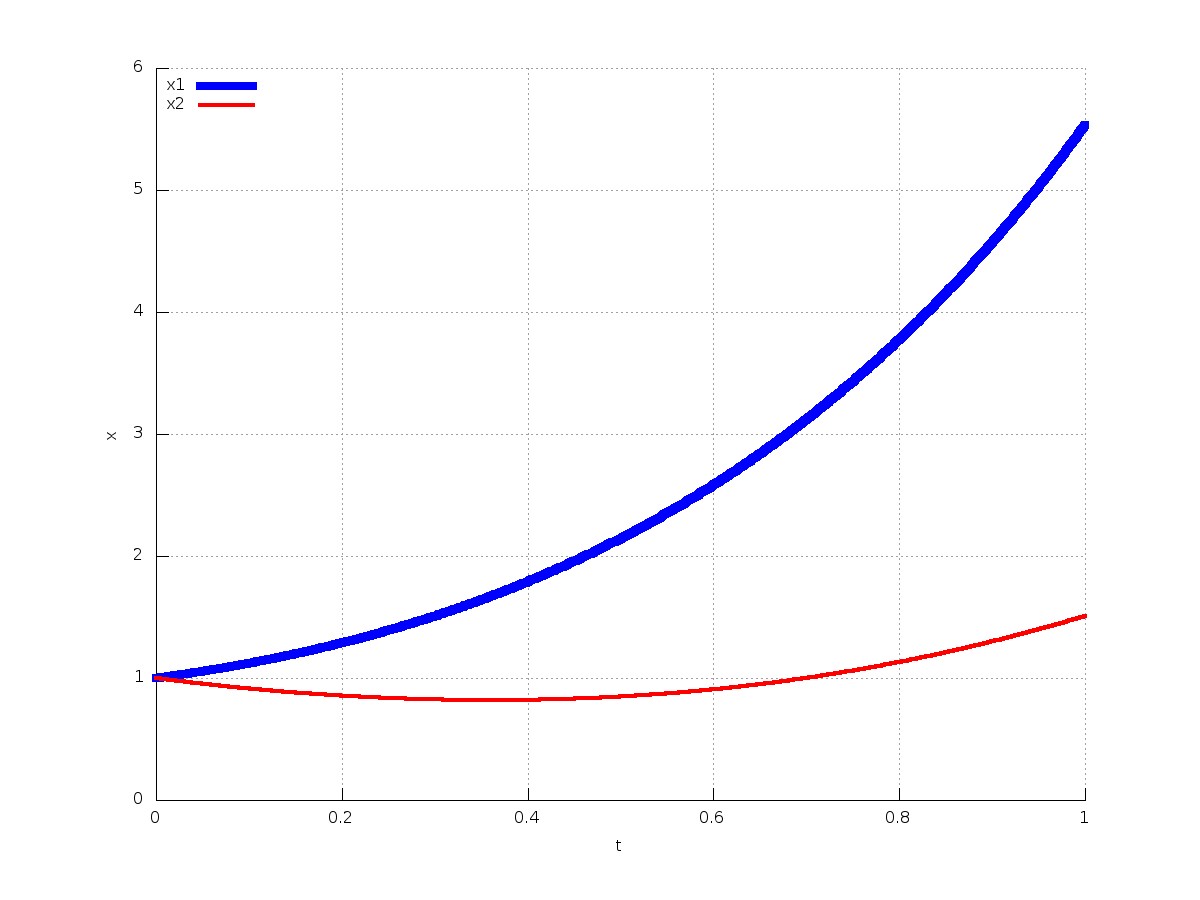
Το γράφημα μπορεί να γίνει ως εξής:
clear;
set (gca, 'fontsize', 24)
function xdot = f(x,t)
xdot(1) = 2*x(1) - x(2) + t;
xdot(2) = x(1) - x(2)^2 - 1;
end
x0 = [1, 1]';
t = linspace(0, 1, 51);
x = lsode('f', x0, t);
plot(t, x(:,1), 'b', 'Linewidth', 8, t, x(:,2), 'r', 'Linewidth', 4);
box off;
grid on;
xlabel 't';
ylabel 'x';
legend ('x1', 'x2', 'Location', 'NorthWest');
print -depsc2 -landscape lsode2.eps
print -djpg lsode2.jpg
Ο πίνακας τιμών της λύσης:
octave:> [t' x ] ans = 0.00000 1.00000 1.00000 0.02000 1.02081 0.98059 0.04000 1.04325 0.96236 0.06000 1.06739 0.94527 0.08000 1.09325 0.92931 0.10000 1.12089 0.91445 0.12000 1.15036 0.90069 0.14000 1.18171 0.88801 0.16000 1.21500 0.87641 0.18000 1.25027 0.86589 0.20000 1.28760 0.85644 ..............................
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.