Υπολογισμός της ισορροπίας της αγοράς με το Octave/Matlab
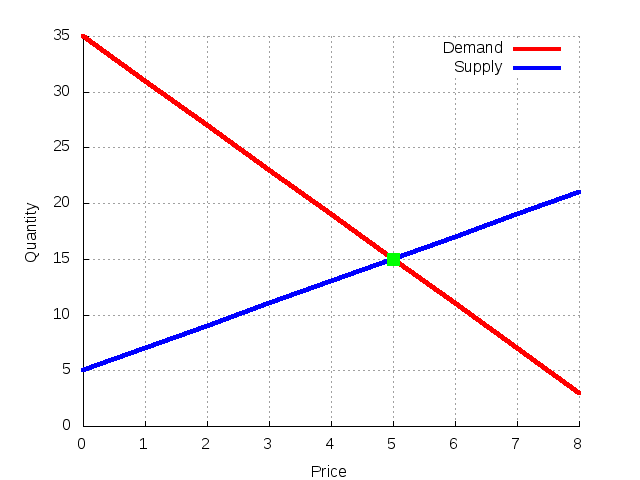
Έστω οι καμπύλες ζήτησης και προσφοράς:
$$ \begin{array}{l l} q^D &= 35 - 4\, p \\ q^S &= 5 +2\, p \end{array} $$
Το σύστημα εξισώσεων μπορεί να γραχεί ως:
$$ \begin{array}{l l} q + 4\, p &= 35 \\ q - 2\, p &= 5 \\ \end{array} $$
Και να λυθεί ως:
$$ \mathbf{A} = \begin{pmatrix} 1 & 4 \\ 1 & -2 \end{pmatrix} \quad , \quad \mathbf{b} = \begin{pmatrix} 35 \\ 5 \end{pmatrix} \quad , \quad \mathbf{x} = \mathbf{A}^{-1} \mathbf{b} $$
a = 35; b = 4; c = 5; d = 2; A = [1 b; 1 -d]; B = [a; c]; x = inv(A) * B; >> qstar = x(1) qstar = 15.000 >> pstar = x(2) pstar = 5
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.