Υπολογισμός με το Maxima του πλεονάσματος παραγωγού και καταναλωτή στην ισορροπία της αγοράς

Έστω πως η ζήτηση και η προσφορά ενός προϊόντος περιγράφονται από τις καμπύλες:
p = 20 -5q
p = 2 + 4q

$$ \begin{align*} p^D &= 20 - 5\, q \\ p^S &= 2 + 4\, q \end{align*} $$

Το ζητούμενο είναι να υπολογίσουμε το πλεόνασμα του παραγωγού και το πλεόνασμα του καταναλωτή στην ισορροπία της αγοράς, το λόγο τους, καθώς και το συνολικό πλεόνασμα.

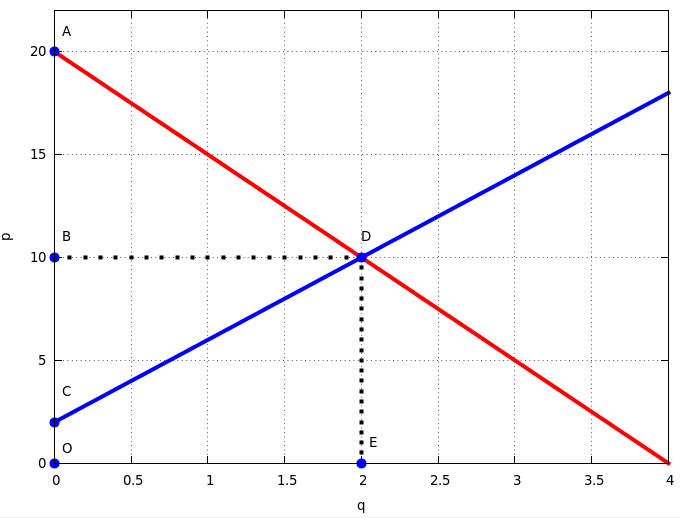
Surplus

Στο παραπάνω σχήμα το πλεόνασμα του παραγωγού αντιστοιχεί στην τριγωνική περιοχή BCD και το πλεόνασμα του καταναλωτή στην τριγωνική περιοχή ABD. Τα δύο αυτά τρίγωνα είναι ορθογώνια και έχουν κοινό ύψος το τμήμα BD.

Υπενθυμίζεται πως το εμβαδόν τριγώνου μπορεί να υπολογιστεί ως εξής:

$$ E = \frac{1}{2} \times \text{Βάση} \times \text{Ύψος} $$

Εργαζόμαστε λοιπόν ως εξής:

Ορίζουμε τις συναρτήσεις που αντιστοιχούν στις καμπύλες ζήτησης και προσφοράς:
```
D(q) := 20 - 5*q;
S(q) := 2 + 4*q;
```
Υπολογίζουμε την ποσόσητα προϊόντος που αντιστοιχεί στο σημείο ισορροπίας:
```
sol : solve(D(q)=S(q), q);
q0 : rhs(sol[1]);
```
Σημείωση: Η ποσότητα q0 αντιστοιχεί στο τμήμα OE το οποίο είναι ίσο με το τμήμα BD:
$$ q_0 = OE = BD $$
Το τμήμα AB μπορεί να υπολογιστεί ως εξής:
$$ D(0) - D(q_0) $$ Επομένως το εμβαδόν τριγώνου που αντιστοιχεί στο πλεόνασμα του καταναλωτή μπορεί να υπολογιστεί ως εξής:
```
CS : (1/2) * (D(0)-D(q0)) * q0;
```
Το τμήμα BC μπορεί να υπολογιστεί ως εξής:
$$ S(q_0) - S(0) $$ Επομένως το εμβαδόν τριγώνου που αντιστοιχεί στο πλεόνασμα του παραγωγού μπορεί να υπολογιστεί ως εξής:
```
PS : (1/2) * (S(q0)-S(0)) * q0;
```
Το τμήμα AB μπορεί να υπολογιστεί ως εξής:
$$ D(0) - D(q_0) $$ Επομένως το εμβαδόν τριγώνου που αντιστοιχεί στο πλεόνασμα του καταναλωτή μπορεί να υπολογιστεί ως εξής:
```
CS : (1/2) * (D(0)-D(q0)) * q0;
```
Ο λόγος των δύο πλεονασμάτων μπορεί να υπολογιστεί ως εξής:
```
CS/PS;
```
Το συνολικό πλεόνασμα μπορεί να υπολογιστεί ως εξής:
```
TS : CS + PS;
```
Ή απευθείας ως το εμβαδόν του τριγώνου ACD:
```
TS :(1/2) * (D(0)-S(0)) * q0;
```

Περαιτέρω εξάσκηση: Υπολογίστε το πλεόνασμα του παραγωγού και του καταναλωτή όταν η αγορά ενός προϊόντος περιγράφεται από τις καμπύλες:
p = 20 -4q
p = 5 + 2q

$$ \begin{align} p^D &= 20 -4\, q \\ p^S &= 5 + 2\, q \end{align} $$ Υπολογίστε επίσης την ελαστικότητα ζήτησης ως προς την τιμή σε αυτό το σημείο.

Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον Αθανάσιο Σταυρακούδη σας παρέχετε κάτω από την άδεια Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.

Athanassios Stavrakoudis, Sat 23 Nov 2024