Αριθμητικός υπολογισμός ρίζας με τη μέθοδο της εφαπτομένης στη C++

Το βίντεο έχει διάρκεια 24:04. Πιθανά να χρειάζεται λίγος χρόνος για την προβολή του.

C++ πρόγραμμα αριθμητική μέθοδος ρίζα εξίσωση προσέγγιση σύγκλιση μέθοδος εφαπτομένης secant method

Έστω πως θέλουμε να υπολογίσουμε μια ρίζα του πολυωνύμου:

$$ {x}^{3}-6\,{x}^{2}-x+30 = 0 $$

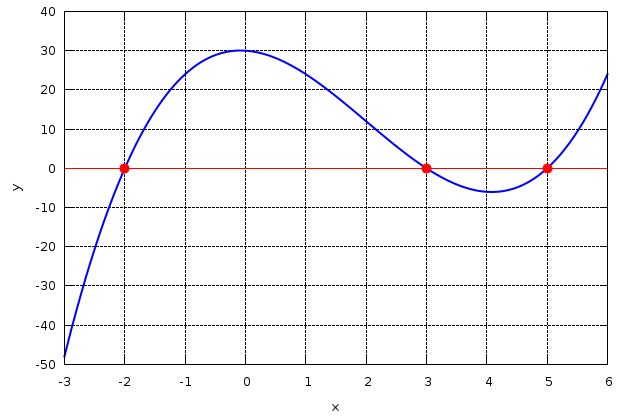
secant method

Η μέθοδος της εφαπτομένης αποτελεί -κατά κάποιο τρόπο- παραλλαγή της μεθόδου Newton–Raphson και βασίζεται σε μια επαναληπτική διαδικασία. Στη μέθοδο Newton–Raphson χρησιμοποιείται η παράγωγος για να εκτιμηθεί μια καλύτερη προσέγγιση της ρίζας:
$$ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $$

Στη μέθοδο της εφαπτομένης, θεωρούμε πως ο λόγος:
$$ \frac{f(x_{n})-f(x_{n-1})} {x_{n}-x_{n-1}} $$
αποτελεί μια καλή προσέγγιση της παραγώγου.

Έτσι ο αναδρομικός τύπος της ακολουθίας είναι:
$$ x_{n+1} = x_n - \frac{f(x_{n}) (x_{n}-x_{n-1})} {f(x_{n})-f(x_{n-1})} = x_n - f(x_{n}) \frac{\Delta x} {\Delta y} $$

Η διαδικασία επαναλαμβάνεται μέχρι να πάρουμε μια ικανοποιητική προσέγγιση. Συνήθως σταματάμε όταν:
$$ |x_{n+1} - x_n| < \epsilon $$

Ακολουθεί ένα παράδειγμα υλοποίησης:

#include <iostream>
#include <stdio.h>
#include <math.h>

using namespace std;

#define MAXITER 100

const double eps = 1e-4;

double f (double x)
{
    return x*x*x - 6*x*x - x + 30;
}

int main()
{
    bool rootFound = false;
    double x[MAXITER];
    double Dx, Dy;
    double d;
    int    i = 2;

    cout << "Εύρεση ρίζας με τη μέθοδο της εφαπτομένης." << endl;
    cout << "------------------------------------------" << endl;

    cout << "Αρχική τιμή x[0]: ";
    cin >> x[0];
    cout << "Αρχική τιμή x[1]: ";
    cin >> x[1];

    printf("    i     x              f(x)           d\n");
    printf("--------------------------------------------------\n");
    do
    {
        Dx     = x[i] - x[i-1];
        Dy     = f(x[i]) - f(x[i-1]);
        x[i+1] = x[i] - f(x[i]) * Dx / Dy;
        d      = fabs(Dx);
        printf("%5d %14.8f %14.8f %14.8f\n", i, x[i+1], f(x[i+1]), d);

        if (d < eps)
        {
            rootFound = true;
            break;
        }

        i++;
        if (i >= MAXITER)
        {
            rootFound = false;
            break;
        }


    } while (rootFound == false);

    if (rootFound == true)
        printf("\nΒρέθηκε x=%.14f\n", x[i]);
    else
        printf("\nΔεν βρέθηκε ρίζα\n");

    return 0;
}

Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον Αθανάσιο Σταυρακούδη σας παρέχετε κάτω από την άδεια Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.

Athanassios Stavrakoudis, Sat 23 Nov 2024