Αριθμητικός υπολογισμός ρίζας πολυωνύμου με τη μέθοδο διχοτόμησης στη C++

Το βίντεο έχει διάρκεια 45:35. Πιθανά να χρειάζεται λίγος χρόνος για την προβολή του.

C++ πρόγραμμα αριθμητική μέθοδος ρίζα εξίσωση προσέγγιση σύγκλιση μέθοδος διχοτόμου bisection

Έστω πως θέλουμε να υπολογίσουμε μια ρίζα του πολυωνύμου:

$$ {x}^{3}-6\,{x}^{2}-x+30 = 0 $$

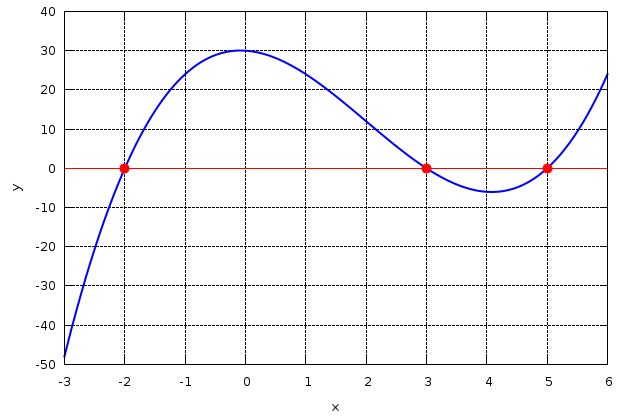
netwton root

Η μέθοδος βασίζεται σε μια επαναληπτική διαδικασία:

Λάβε τα αρχικά σημεία $x_1, x_2$
Αν $f(x_1)=0$ ή $f(x_2)=0$ επέστρεψε τη ρίζα και τερμάτισε τη διαδιασία
Αν οι τιμές $f(x_1), f(x_2)$ είναι ομόσημες τερμάτισε τη διαδικασία
Υπολόγισε το μέσο $x=\frac{1}{2} (x_1+x_2)$
Υπολόγισε την τιμή f(x)
Αν η απόλυτη τιμή της διαφοράς $|x_2-x_1|$ είναι πολύ μικρή, ή $f(x)=0$, επέστρεψε το $x$ και τερμάτισε την επανάληψη
Αν $f(x)f(x_1) > 0$ θέσε $x_1=x$, αλλιώς αν $f(x)f(x_1) < 0$ θέσε $x_2=x$, επανέλαβε από το σημείο 4

Ακολουθεί ένα παράδειγμα υλοποίησης:

#include <iostream>
#include <math.h>
#include <stdio.h>

using namespace std;

#define MAXREP 10

const double tol = 1e-6;

double f(double x)
{
    return x*x*x - 6*x*x - x + 30;
}

int main()
{
    bool rootFound = false;
    double x1, x2, x;
    double y1, y2, y;
    int i = 1;

    cout << "Υπολογισμός ρίζας με τη μέθοδο της διχοτόμησης." << endl;
    cout << "Δώσε τα όρια [x1,x2] για την εύρεση της ρίζας." << endl;
    cout << "-------------------------------------------------------" << endl;

    cout << "Δώσε το x1: ";
    cin >> x1;
    cout << "Δώσε το x2: ";
    cin >> x2;
    cout << "-------------------------------------------------------" << endl;

    y1 = f(x1);
    y2 = f(x2);

    if (y1 == 0)
    {
        x = x1;
        rootFound = true;
    }
    else if (y2 == 0)
    {
        x = x2;
        rootFound = true;
    }
    else if (y1*y2 > 0)
    {
        cout << "Οι τιμές y1, y2 έχουν το ίδιο πρόσημο." << endl;
        cout << "Η μέθοδος διχοτόμησης δεν μπορεί να εφαρμοστεί." << endl;
        return 0;
    }
    else
    {
        printf("     i              x              y\n");
        printf("------------------------------------\n");

        do
        {
            x = 0.5 * (x1 + x2);
            y = f(x);
            printf("%6d %14.8f %14.8f \n", i, x, y);

            if (y == 0)
            {
                rootFound = true;
                break;
            }
            else if  (y*y1 > 0)
                x1 = x;
            else
                x2 = x;

            y1 = f(x1);

            if (0.5*fabs(x2-x1) < tol)
            {
                rootFound = true;
                break;
            }

            if (i >= MAXREP)
            {
                 cout << "\nSTOP: Ξεπεράστηκε το μέγιστο πλήθος επαναλήψεων.\n"<< endl;
                 break;
            }

            i++;

        } while (rootFound == false);
    }

    if (rootFound == true)
        printf("\nΒρέθηκε  x=%.14f\n", x);

    return 0;
}

Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον Αθανάσιο Σταυρακούδη σας παρέχετε κάτω από την άδεια Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.

Athanassios Stavrakoudis, Thu 18 Apr 2024