Υπολογισμός συνάρτησης ελαστικότητας ως προς την τιμή από την καμπύλη ζήτησης με το Maxima

Εδώ τα δεδομένα είναι:

Η καμπύλη ζήτησης, μια σχέση της μορφής
$$ p = f(q) $$
Ένα ή περισσότερα σημεία πάνω στο κάθετο άξονα της τιμής

Τα ζητούμενα είναι:

Η κατασκευή της συνάρτησης ελαστικότητας ως προς την τιμή, μια σχέση της μορφής
$$ E_D = f(p) $$
Ο υπολογισμός της ελαστικότητας σημείου σε ένα ή περισσότερα σημεία.

Γενικό παράδειγμα:

Έστω πως η καμπύλη ζήτησης δίνεται από τη γραμμική σχέση:
$$p=a-b\,q$$

Και πως θέλουμε να υπολογίσουμε την ελαστικότητα ζήτησης ως προς την τιμή στο σημείο:
$$ p = P_0 $$

Λύση:

D     : p = a - b*q;
sol   : solve (D, q);
D(p)  := ''(rhs(sol[1]));
Ed(p) := ''( p / D(p) * diff(D(p), p) );
Ed(P0);

Ειδικό παράδειγμα:

Έστω πως η καμπύλη ζήτησης δίνεται από τη γραμμική σχέση:
$$p=20-4\,q$$

Και πως θέλουμε να υπολογίσουμε την ελαστικότητα ζήτησης ως προς την τιμή στα σημεία:
$$ p_0 = 10, \quad p_2 = p_0 - 5, \quad p_2 = p_0 + 5 $$

Λύση:

D     : p = 20 - 4*q;
p0    : 10;
sol   : solve (D, q);
D(p)  := ''(rhs(sol[1]));
Ed(p) := ''( p / D(p) * diff(D(p), p) );
Ed(p0);
Ed(p0-5); 
Ed(p0+5);

Σημείωση: Και στις δύο περιπτώσεις το κλειδί για τη λύση είναι η κατασκευή της συνάρτησης ζήτησης από την καμπύλη ζήτησης και στη συνέχεια ο ορισμός της συνάρτησης ελαστικότητας ζήτησης ως προς την τιμή, Ed(p).

Επιπλέον εξάσκηση: Στο παραπάνω παράδειγμα ειδικής λύσης
$$p = 20 - 4 \, q$$
δείξτε πως ισχύει
$$ E_D(p_0-p_C) \times E_D(p_0+p_C) = 1 $$
για κάθε $$p_C$$ (όχι μόνο για $$p_C=5$$), με την προϋπόθεση πως p0 είναι το σημείο μοναδιαίας ελαστικότητας, όπως ισχύει στο παραπάνω παράδειγμα ($$p_0=10$$).

Γεωμετρικός υπολογισμός της ελαστικότητας σημείου

Αν κάνετε την άσκηση της γενικής περίπτωσης, τότε θα βρείτε πως για μια γραμμική καμπύλη ζήτησης της μορφής
$$ p = a - b\,q $$
τότε η ελαστικότητα σημείου ζήτησης ως προς την τιμή δίνεται από τη σχέση:
$$ E_d = \cfrac{p}{p-a} $$
όπως φαίνεται στο παρακάτω σχήμα:
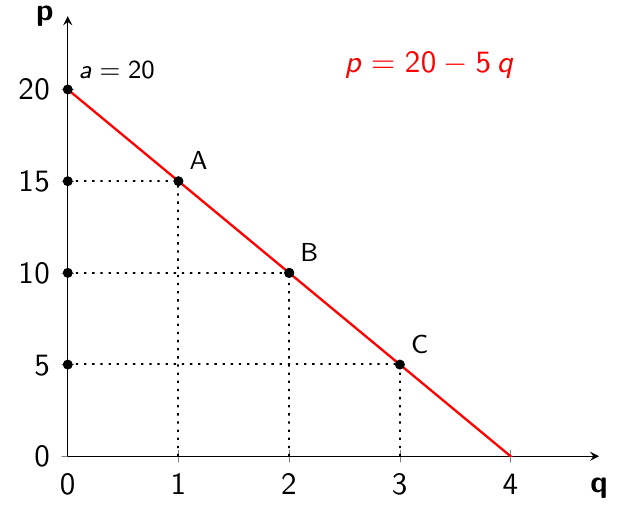
Γεωμετρικός υπολογισμός της ελαστικότητας σημείου

Για παράδειγμα, η ελαστικότητα ζήτησης ως προς την τιμή στο σημείο $$p_A=15$$ υπολογίζεται ως εξής:
$$ E_d = \cfrac{15}{15-20} = \cfrac{15}{-5} = -3 $$
δηλαδή το σημείο Α είναι στην ελαστική περιοχή της καμπύλης ζήτησης.

Επίσης, η ελαστικότητα ζήτησης ως προς την τιμή στο σημείο $$p_C=5$$ υπολογίζεται ως εξής:
$$ E_d = \cfrac{5}{5-20} = \cfrac{5}{-15} = -\cfrac{1}{3} $$
δηλαδή το σημείο C είναι στην ανελαστική περιοχή της καμπύλης ζήτησης.

Τέλος, η ελαστικότητα ζήτησης ως προς την τιμή στο σημείο $$p_B=10$$ υπολογίζεται ως εξής:
$$ E_D = \cfrac{10}{10-20} = \cfrac{10}{-10} = -1 $$
δηλαδή το σημείο B είναι το σημείο μοναδιαίας ελαστικότητας. Προφανώς, εφόσον ισχύει
$$p_B = \dfrac{a}{2}$$

Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον Αθανάσιο Σταυρακούδη σας παρέχετε κάτω από την άδεια Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.

Athanassios Stavrakoudis, Sat 23 Nov 2024