Ολοκλήρωση με τη μέθοδο Monte Carlo με το Excel/Calc
Να προγραμματίσετε ένα φύλλο εργασίας για τον υπολογισμό του ορισμένου ολοκληρώματος y = ex στο διάστημα [0,b] όπου b πραγματικός αριθμός στο διάστημα [1,20]. Να χρησιμοποιήσετε τη μέθοδο monte carlo για την αριθμητική εκτίμηση του ολοκληρώματος.
Η μέθοδος χρησιμοποιείται γενικά για ορισμένα ολοκληρώματα. Αυτό σημαίνει πως τα όρια είναι γνωστά, πχ [a,b]. Αυτό που ζητάει η εκφώνηση, για μεταβλητό άνω όριο b, μπορεί εύκολα να προγραμματιστεί θέτοντας μια τιμή σε ένα κελί.
Η μέθοδος απαιτεί την κατασκευή Ν τυχαίων σημείων. Οι συντεταγμένες προέρχονται από τυχαίους αριθμούς ομοιόμορφης κατανομής.
Για την τετμημένη (x) παίρνουμε έναν τυχαίο αριθμό στο διάστημα [a,b].
Για την τεταγμένη (y) παίρνουμε έναν τυχαίο αριθμό στο διάστημα [ymin, ymax], δηλαδή ανάμεσα στην ελάχιστη και τη μέγιστη τιμή που έχει η συνάρτηση στο διάστημα [a,b]. Αν αυτό δεν είναι δυνατό να υπολογιστεί επακριβώς, τότε είτε το αντιλαμβανόμαστε από το γράφημα της συνάρτησης, είτε θέτουμε εικονικό ελάχιστο, μικρότερο από το πραγματικό ελάχιστο και εικονικό μέγιστο, μεγαλύτερο από το πραγματικό μέγιστο. Θα πρέπει δηλαδή να περικλείσουμε την επιφάνεια για την οποία ενδιαφερόμαστε με ορθογώνιο παραλληλόγραμμο μεγαλύτερο, και όχι μικρότερο από την επιφάνεια.
Τελικά έχουμε Ν σημεία, ομοιόμορφα διεσπαρμένα στην επιφάνεια ενός ορθογωνίου παραλληλογράμμου με επιφάνεια E = (b-a)*(ymax-ymin), ή E = Δx*Δy.
Για κάθε τυχαίο x, υπολογίζουμε το πραγματικό y (yt), το οποίο δεν ταυτίζεται με το αντίστοιχο τυχαίο y (yr). Ελέγχοντας την παράσταση:
$$ y_r \le y_t $$
Υπολογίζουμε το πλήθος των σημείων (N1), τα οποία βρίσκονται μέσα στην περιοχή που αντιστοιχεί στο ολοκλήρωμα της συνάρτησης.
Το ολοκκλήρωμα δίνεται από τη σχέση:
$$ I = \frac{N1}{N} \times E $$
Η μέθοδος εφαρμόζεται για συνεχείς και φραγμένες συναρτήσεις εντός των ορίων [a,b].
Η ακρίβειά της αυξάνεται όσο αυξάνεται το πλήθος των σημείων και όσο μικρότερο είναι το ορθογώνιο που περικλείει την επιφάνεια του ολοκληρώματος προς υπολογισμού.
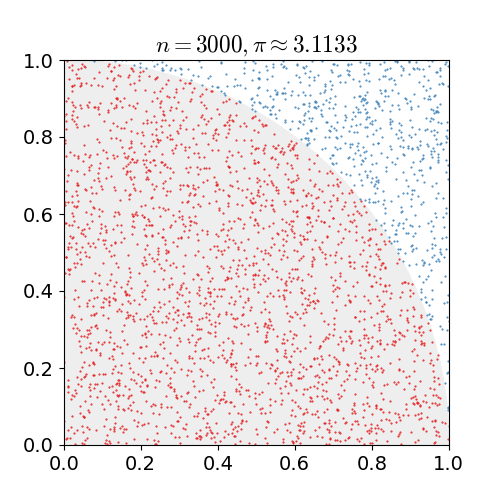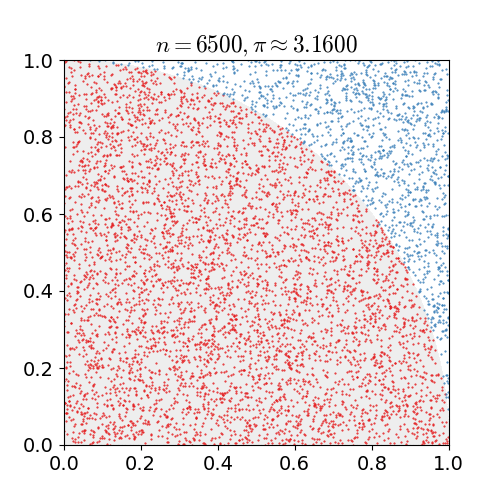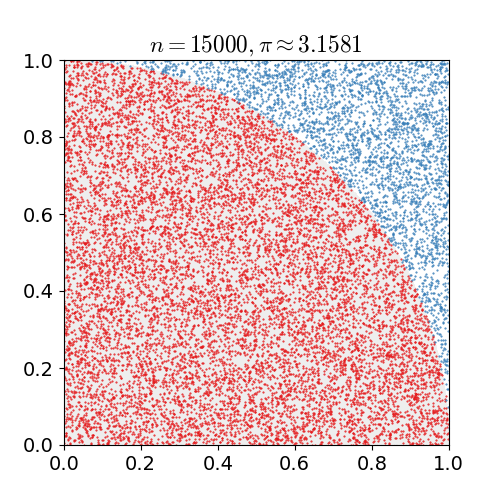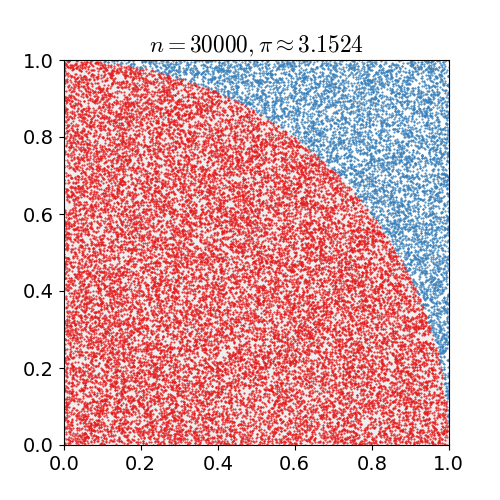
Η παρακάτω εικόνα δείχνει παραστατικά της εφαρμογή της μεθόδου για το ολοκλήρωμα
$$ \int_0^{\pi/4} \sqrt{1-x^2} \, dx $$
για τον υπολογισμό του π (η εξίσωση κύκλου είναι η x^2+y^2=1). Η εικόνα προέρχεται από την ιστοσελίδα: http://en.wikipedia.org/wiki/Monte_Carlo_method
Επισυναπτόμενα αρχεία για μεταφόρτωση (download)
Ερωτήματα επιλογής SQL με λογική σύζευξη και διάζευξησχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.