Διαγράμματα ισοϋψών καμπυλών (contour plots) στο Octave/Matlab
Τρισδιάστατο γράφημα με προβολή ισοϋψών καμπυλών
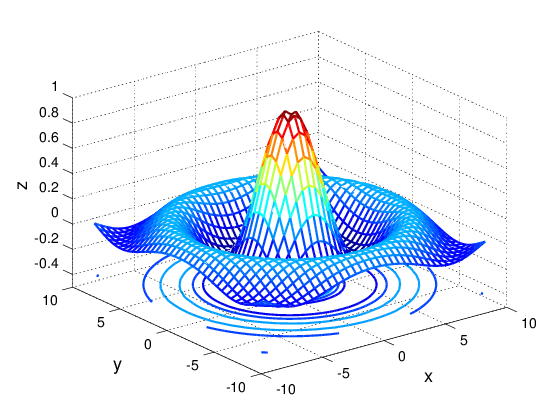
clear; clf;
x = -9:0.5:9;
y = -9:0.5:9;
[X, Y] = meshgrid (x, y);
r = sqrt (X .^ 2 + Y .^ 2);
Z = sin (r) ./ r;
meshc(X, Y, Z, 'LineWidth', 2);
grid on;
box off;
xlabel("x", 'FontWeight', 'bold', 'FontSize', 18);
ylabel("y", 'FontWeight', 'bold', 'FontSize', 18);
zlabel("z", 'FontWeight', 'bold', 'FontSize', 18);
set(gca, 'FontWeight', 'bold', 'FontSize', 14);
axis([-10, 10, -10, 10, -0.5, 1]);
Μορφοποίηση τρισδιάστατου διαγράμματος ισοϋψών καμπυλών
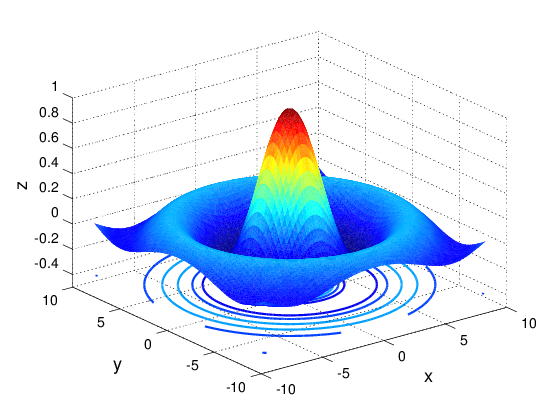
clear; clf;
x = -9:0.25:9;
y = -9:0.25:9;
[X, Y] = meshgrid (x, y);
r = sqrt (X .^ 2 + Y .^ 2);
Z = sin (r) ./ r;
meshc(X, Y, Z, 'LineWidth', 2);
grid on;
box off;
xlabel("x", 'FontWeight', 'bold', 'FontSize', 18);
ylabel("y", 'FontWeight', 'bold', 'FontSize', 18);
zlabel("z", 'FontWeight', 'bold', 'FontSize', 18);
set(gca, 'FontWeight', 'bold', 'FontSize', 14);
axis([-10, 10, -10, 10, -0.5, 1]);
shading flat;
colormap(jet);
Διάγραμμα ισοϋψών καμπυλών σε 2 διαστάσεις (contour plot)
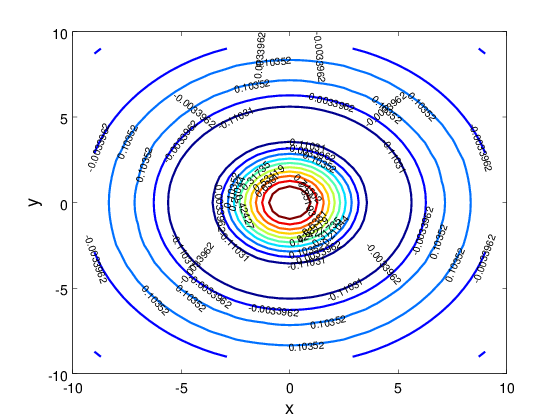
clear; clf;
x = -9:0.5:9;
y = -9:0.5:9;
[X, Y] = meshgrid (x, y);
r = sqrt (X .^ 2 + Y .^ 2);
Z = sin (r) ./ r;
contour(X, Y, Z, 10, 'Linewidth', 2, 'ShowText','on');
xlabel("x", 'FontWeight', 'bold', 'FontSize', 18);
ylabel("y", 'FontWeight', 'bold', 'FontSize', 18);
set(gca, 'FontWeight', 'bold', 'FontSize', 14);
axis([-10, 10, -10, 10]);
Μορφοποίηση διαγράμματος ισοϋψών καμπυλών σε 2 διαστάσεις (contour plot)
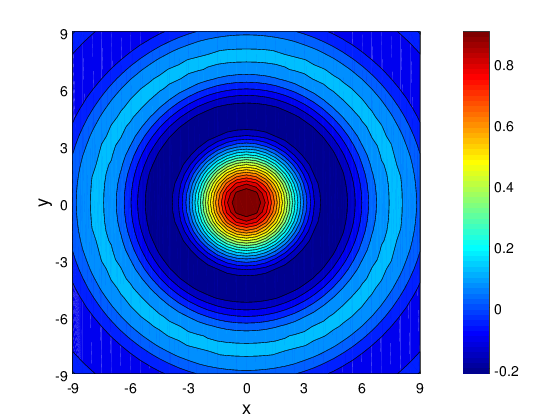
clear; clf;
x = -9:0.5:9;
y = -9:0.5:9;
[X, Y] = meshgrid (x, y);
r = sqrt (X .^ 2 + Y .^ 2);
Z = sin (r) ./ r;
contourf(X, Y, Z, 20);
xlabel("x", 'FontWeight', 'bold', 'FontSize', 18);
ylabel("y", 'FontWeight', 'bold', 'FontSize', 18);
set(gca, 'FontWeight', 'bold', 'FontSize', 14);
axis([-9, 9, -9, 9]);
set(gca,'XTick', -9:3:9);
set(gca,'YTick', -9:3:9);
colormap(jet);
colorbar('EastOutside', 'FontWeight', 'bold', 'FontSize', 14);
Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.