Υπολογισμός του π με προσομοίωση Monte Carlo με την R
Ο υπολογισμός του π με χρήση τυχαίων αριθμών ομοιόμορφης κατανομής, είναι μια χρήσιμη εξάσκηση σε οποιοδήποτε πρόγραμμα.
Η εξίσωση του μοναδιαίου κύκλου είναι
$$ x^2 + y^2 =1 $$
και για το πρώτο τεταρτημόριο (θετικό x, θετικό y) ισχύει:
$$ y = \sqrt{1 - x^2}, \; \; r = x^2 + y^2 $$
όπου r η απόσταση ενός σημείου από το κέντρο των αξόνων. Αν r < 1 τότε το σημείο κείται εντός του μοναδιαίου κύκλου.
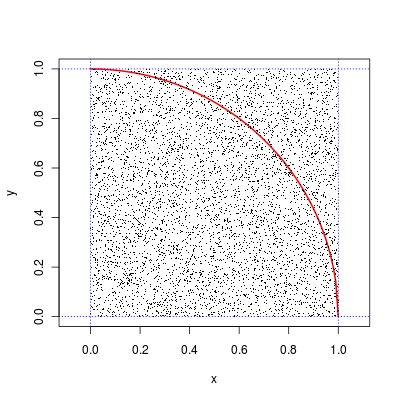
Το π/4 μπορεί να υπολογιστεί ως ο λόγος των σημείων που κείτονται κάτω της καμπύλης, ως προς το σύνολο των σημείων.
N <- 10000 x <- runif(N) y <- runif(N) r <- x^2 + y^2 N1 <- sum(r<1) myPi <- 4*N1/N myPi [1] 3.114
Η προσέγγιση που θα πάρετε μπορεί να διαφέρει λίγο από 3.114 που βρήκα εγώ. Διαφορετικά δείγματα τυχαίων αριθμών θα δώσουν διαφορετικά αποτελέσματα.
Αν θέλετε να κατασκευάσετε το παραπάνω γράφημα, έχει λίγο κόπο, αλλά μπορείτε να το κάνετε έτσι:
x <- seq(0, 1, by=0.01) y <- sqrt(1-x^2) plot(x, y, type="l", asp=1,xlim=c(0,1), ylim=c(0,1), col=2, lwd=2) abline(h=0, col="blue", lty=3) abline(v=0, col="blue", lty=3) abline(h=1, col="blue", lty=3) abline(v=1, col="blue", lty=3) N <- 10000 x <- runif(N) y <- runif(N) points(x, y, type="p", cex=0.2, pch=18)
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.