Γράφημα συνάρτησης και της εφαπτομένης της σε σημείο με το Maxima
Έστω μια συνάρτηση f(x), και g(x) η παράγωγός της. Έστω x=a ένα σημείο στον οριζόντιο άξονα. Θέλουμε να κατασκευάσουμε το γράφημα της καμπύλης f(x) καθώς και την ευθεία της εφαπτομένης στο σημείο x=a.
Ορισμός μιας συνάρτησης:
f(x):= x^2-6*x+20;
Ορισμός ενός σημείου στον οριζόντιο άξονα:
a : 4;
Η παράγωγος και η εξίσωση της ευθείας της παραγώγου που περνά από το σημείο:
g(x) := ''( diff(f(x), x) ); h(x) := ''( g(a)*x+f(a)-a*g(a) );
Γράφημα της συνάρτησης και της εφαπτομένης στο καθορισμένο σημείο:
plot2d([f(x), h(x)], [x, a-5, a+5], [ylabel, "f(x)"] );
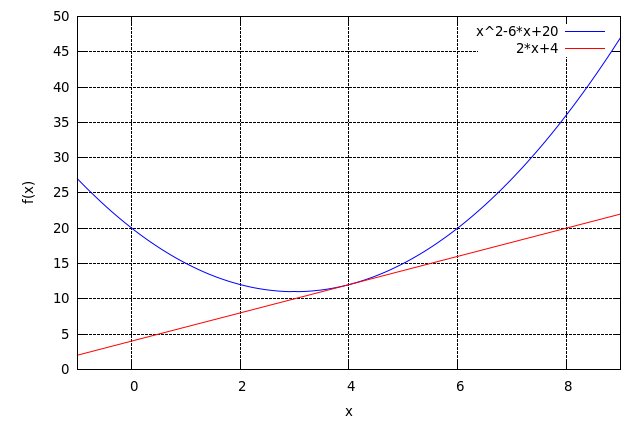
Η επιλογή [x, a-5, a+5] είναι ενδεικτική και δηλώνει το εύρος του οριζόντιου άξονα στο γράφημα.
Τόσο η συνάρτηση, όσο και το σημείο είναι επίσης ενδεικτικά. Μπορείτε εύκολα να τα αλλάξετε και να πάρετε ένα νέο γράφημα.
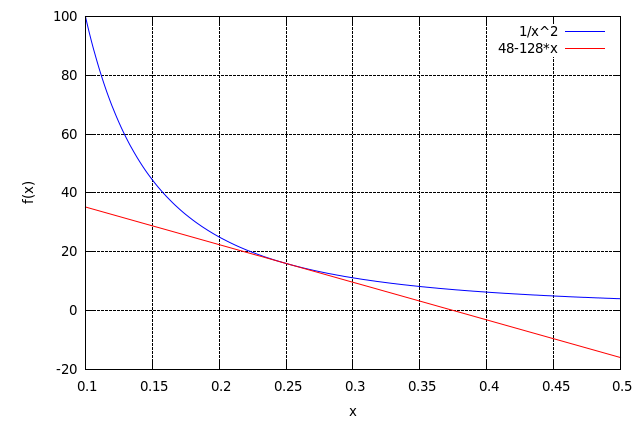
Γεια παράδειγμα να κάνετε το γράφημα της συνάρτησης f(x) = 1/x^2 και να φέρετε την ευθεία της εφαπτομένης στο σημείο χ=1/4:
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.