Επίλυση της μονοπωλιακής αγοράς με το Maxima
Έστω η καμπύλη ζήτησης για ένα προϊόν το οποίο παράγεται από κάποιο μονοπώλιο:
$$ p = 150 - 5q $$
Το μονοπώλιο παράγει το προϊόν με ολικό κόστος:
$$ TC = 50 q $$
Να υπολογιστεί το επίπεδο παραγωγής και το κέρδος του μονοπωλίου.
Η καμπύλη ζήτησης για το μονοπωλιακό προϊόν:
D(q) := 150-5*q;
Το οριακό έσοδο ορίζεται ως:
MR(q) := ''(diff(q*D(q), q));
Έστω το ολικό κόστος δίνεται από τη σχέση:
TC(q) := 50*q;
Το οριακό κόστος είναι ίσο με:
MC(q) := ''(diff(TC(q), q));
Το μέσο κόστος είναι ίσο με:
AC(q) := ''(TC(q)/q);
Η ποσότητα του παραγόμενου προϊόντος του μονοπωλίου:
sol : solve(MR(q) = MC(q), q); q0 : rhs(sol[1]);
Η αντίστοιχη τιμή στην ισορροπία:
p0: D(q0);
η συνάρτηση κέρδους του μονοπωλίου:
pi(p,q):= (p-AC(q))*q;
στην ισορροπία είναι:
pi(p0, q0);
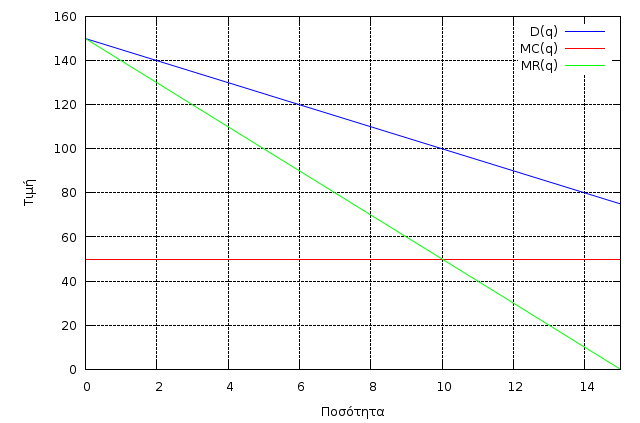
Διαγραμματική αναπαράσταση:
plot2d([D(q), MC(q), MR(q)],[q,0,15], [xlabel, "Ποσότητα"], [ylabel, "Τιμή"], [legend, "D(q)", "MC(q)", "MR(q)"]);
Επιπλέον εξάσκηση: Να υπολογιστεί η σχετική ποσοστιαία μεταβολή στην ποσότητα και τιμή προϊόντος αν υποθέσουμε πως η συνάρτηση ολικού κόστους μεταβάλλεται σε : $$ TC = 40\,q $$
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.