Κινητός μέσος όρος στην R
Έστω μια ακολουθία τιμών :
$$ x_t = x_1, x_2, x_3 \ldots $$
Στην απλή περίπτωση του κινητού μέσου όρου, πχ 3 όρων, ορίζουμε την ακολουθία
$$ m_3 = \frac{x_1+x_2+x_3}{3} \, , \, m_4 = \frac{x_2+x_3+x_4}{3} \, \, $$ κτλ
Υπολογίσουμε δηλαδή το μέσο όρο για 3 διαδοχικές τιμές. Το πλήθος των στοιχείων λέγεται παράθυρο (window), εδώ ίσο με 3. Προφανώς, ανάλογα με την περίπτωση, μπορείτε να έχετε διαφορετικό παράθυρο, πχ 5, 10 ή και 50, 200 κτλ.
Το R δε διαθέτει έτοιμη συνάρτηση για το υπολογισμό του κινητού μέσου όρου. θα χρησιμοποιήσουμε τη συνάρτηση filter, η οποία με κάποιο τρυκ θα αποδώσει τον κινητό μέσο όρο.
Έστω η ακολουθία τιμών 1:10 και πως θέλουμε να υπολογίσουμε τον κινητό μέρο με παράθυρο 3. Δηλαδή το μέσο όρο των 1,2,3, τον μέσο όρο των 2,3,4, τον μέσο όρο των 3,4,5 κτλ κτλ. Να πως γίνεται:
> x <- 1:10 > filter(x, rep(1/3, 3), sides=1) Time Series: Start = 1 End = 10 Frequency = 1 [1] NA NA 2 3 4 5 6 7 8 9
Υπενθυμίζεται πως η συνάρτηση rep() επαναλαμβάνει κάποιες τιμές, εδώ επαναλαμβάνει τρεις φορές το 1/3:
> rep(1/3, 3) [1] 0.33333 0.33333 0.33333
Η επιλογή sides=1 λέει πως λαμβάνονται υπ'όψιν μόνο οι προηγούμενες τιμές, διαφορετικά ο μέσος όρος υπολογίζεται ως προς την κεντρική τιμή. Αν παραλείψουμε την επιλογή θα πάρουμε:
> filter(x, rep(1/3, 3)) Time Series: Start = 1 End = 10 Frequency = 1 [1] NA 2 3 4 5 6 7 8 9 NA
Τελικά, ο τύπος:
> filter(x, rep(1/3, 3), sides=1)
σημαίνει: Φιλτράρισε τα δεδομένα του x ανά 3 με στάθμιση 1/3 (επομένως μέση τιμή) υπολογίζοντας τις 3 προηγούμενες τιμές από την τρέχουσα θέση.
Μια εξαιρετική ιδέα είναι να δοκιμάσετε τον τύπο για διαφορετικά x μέχρι να εξοικιωθείτε με τον υπολογισμό.
Η ανάλυση χρημαστηριακών χρονολογικών σειρών χρησιμοποιεί πολλούς ακόμα τύπους για κινητούς μέσους όρους. Εδώ θα δείξουμε ένα απλό παράδειγμα για λευκό θόρυβο και τυχαίο περίπατο με τον κλασσικό κινητό μέσο όρο.
Ας θεωρήσουμε μια ακολουθία τιμών (χρονολογική σειρά) που είναι λευκός θόρυθος:
x <- rnorm(100)
και ο αντίστοιχος τυχαίος περίπατος που παράγεται από τον λευκό θόρυθο:
y <- cumsum(x)Για παράθυρο ίσο με 10:
w <- 10
Ο κινητός μέσος όρος είναι:
m <- filter(x, rep(1/w, w), sides=1)
Και μπορεί να παρασταθεί γραφικά ως εξής:
plot(x, type="l") lines(m, col=2, lwd=6)
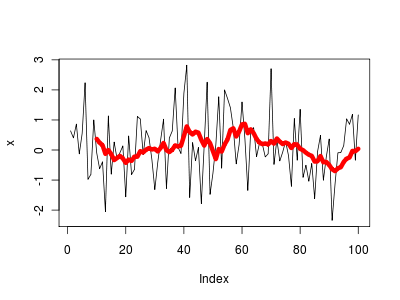
Ο κινητός μέσος όρος του τυχαίου περιπάτου είναι:
m <- filter(y, rep(1/w, w), sides=1)
Και μπορεί να παρασταθεί γραφικά ως εξής:
plot(y, type="l") lines(m, col=2, lwd=6)
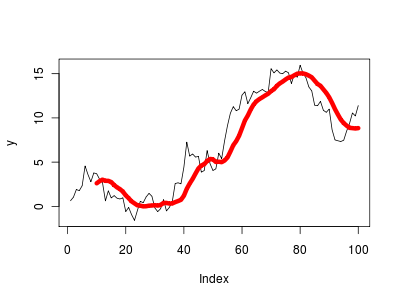
Όπως παρατηρείτε ο κινητός μέσος όρος εξομαλύνει τα δεδομένα.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.