Προσομοίωση διαδικασίας Wiener στο Octave/matlab
Η διαδικασία Wiener $$(W_t)$$ είναι μια στοχαστική διαδικασία συνεχούς χρόνου. Έχει τρεις κύριες ιδιότητες:
- $$W_0 = 0$$
- Η διαδικασία είναι σχεδόν συνεχής
- Αν 0 < s < t < T,
τότε:
$$ W_t - W_s = \sqrt{t-s} N(0,1) $$
Δηλαδή, αν 0 < t < s < u < v < T
τότε:
$$ W_t - W_s $$ και $$ W_v - W_u $$ είναι ανεξάρτητα
Τα βήματα της διαδικασίας Wiener μπορούν να προσομοιωθούν ως:
$$ dW \backsim \sqrt{dt} N(0,1) $$
Πρόκειται για την απλούστερη στοχαστική διαφορική εξίσωση:
$$ dW = \mu dt + \sigma dX $$
Για την υπολογιστική προσομοίωση:
- Παίρνουμε ένα μεγάλο πλήθος στιγμών, πχ 1000
- Μηδενίζουμε το διάνυσμα τιμών W
- Υπολογίζουμε το $$ dW \backsim \sqrt{dt} N(0,1) $$
- Αθροίζουμε το βήματα στο W (cumsum)
- Προαιρετικά, κάνουμε το γράφημα (plot)
clear;
T = 1;
N = 1000;
dt = T/N;
W = zeros(N,1);
dW = sqrt(dt)*randn(N,1);
W = cumsum(dW);
plot(W)
Time = linspace(0, T, N);
plot(Time, W, 'r', "linewidth", 2)
xlabel('Time');
ylabel('W(t)');
grid on;
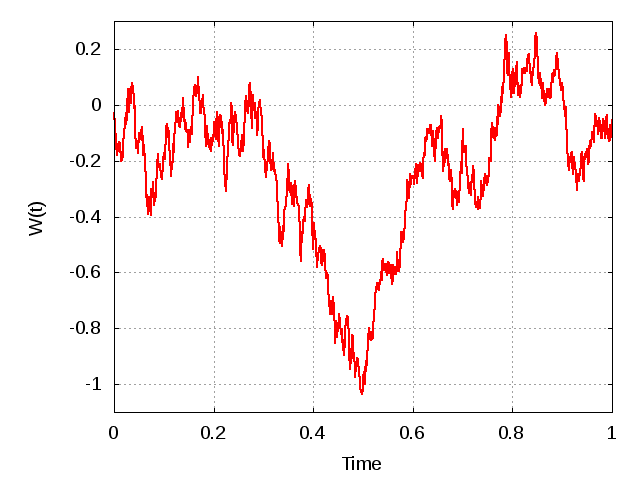
Και μια άσκηση: Να πάρετε τμήματα της διαδικασίας W (πχ ανά 100 στιγμές) και να υπολογίσετε το μέσο και τη διακύμανση. Να παραστήσετε γραφικά ως προς t.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.