Έλεγχος ετεροσκεδαστικότητας στα κατάλοιπα παλινδρόμησης με την R
Ετεροσκεδαστικότητα είναι (γενικά μιλώντας) η μη σταθερή διακύμανση. Θα δούμε ένα παράδειγμα ελέγχου ετεροσκεδαστικότητας με το τεστ Breusch-Pagan.
Θα χρησιμοποιηθούν τεχνητά δεδομένα (προσομοίωση με τυχαίους αριθμούς).
Κατασκευή της σειράς u (ομοσκεδαστικότητα) και της σειράς w (ετεροσκεδαστικότητα):
> T <- 100 > u <- rnorm(T) > w <- rnorm(T, sd=rep(c(1,5), T/2))
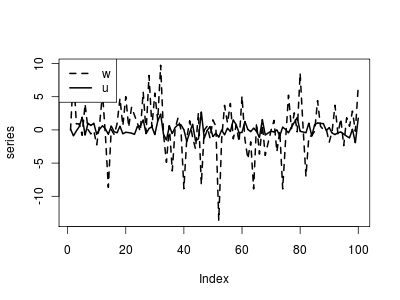
Μια σειρά x, και οι σειρές y1=x+u (ομεσκεδαστικά κατάλοιπα) και y2=z+w (ετεροσκεδαστικά κατάλοιπα):
> x <- rep(1:2, T/2) > y1 <- x + u > y2 <- x + w
Τα κατάλοιπα της παλινδρόμησης του y1 στο x έχουν ομοσκεδαστικότητα (εκ κατασκευής). Ωστόσο, τα κατάλοιπα της παλινδρόμησης του y2 στο x έχουν ετεροσκεδαστικότητα (πάλι εκ κατασκευής). Ο ερευνητής βέβαια που έχει στα χέρια του τις σειρές x,y1,y2 και δε γνωρίζει το μηχανισμό που κατασκεύασε τα u,w πρέπει να κάνει κάποιο διαγνωστικό τεστ για το διαπιστώσει.
Το τεστ bptest της βιβλιοθήκης lmtest χρησιμοποιείται για το σκοπό αυτό:
> library(lmtest)
> f1 <- lm(y1 ~ x)
> f2 <- lm(y2 ~ x)
> bptest(f1)
studentized Breusch-Pagan test
data: y1 ~ x
BP = 0.0179, df = 1, p-value = 0.8934
> bptest(f2)
studentized Breusch-Pagan test
data: y2 ~ x
BP = 19.053, df = 1, p-value = 1.271e-05
Στη δεύτερη περίπτωση, η χαμηλή τιμή p-value = 1.271e-05 υποδεικνύει την απόρριψη της υπόθεσης ομοσκεδαστικότητας.
Μια άλλη δυνατότητα είναι ο έλεγχος μη σταθερής διακύμανσης (ncvTest), υπάρχει στη βιβλιοθήκη car:
> library(car) > ncvTest(f1) Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 0.046835 Df = 1 p = 0.82867 > ncvTest(f2) Non-constant Variance Score Test Variance formula: ~ fitted.values Chisquare = 42.844 Df = 1 p = 5.9278e-11
Η χαμηλή τιμή p = 5.9278e-11, στη δεύτερη περίπτωση, υποδεικνύει την απόρριψη της υπόθεσης σταθερής διακύμανσης στα κατάλοιπα της παλινδρόμησης.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.