Μεγιστοποίηση χρησιμότητας, καμπύλη αδιαφορίας και εφαπτόμενη εισοδηματικού περιορισμού στο Maxima
Η άσκηση προέρχεται από το βιβλίο Μικροοικονομική θεωρία του Walter Nicholson (άσκ. 4.4).
Έστω η συνάρτηση χρησιμότητας:
$$ U(x,y) = \sqrt{x^2+y^2} $$
όπου x,y οι ποσότητες δύο προϊόντων με τιμή Px=3 και Py=4.
- Να βρεθούν οι ποσότητες x,y που μεγιστοποιούν τη χρησιμότητα, αν το εισόδημα είναι I=50
- να γίνει διαγραμματική παράσταση της καμπύλης αδιαφορίας του καταναλωτή και φέρεται την ευθεία του εισοδηματικού περιορισμού που εφάπτεται στην καμπύλη
Λύση
Ορισμός των δεδομένων:
U(x,y) := sqrt(x^2 + y^2); Px : 3; Py : 4; I : 50;
Ορισμός της συνάρτησης Lagrange:
L(x,y,lambda) := U(x,y) + lambda*(I-Px*x-Py*y);
Επίλυση του συστήματος:
eq1: diff(L(x,y,lambda),x)=0; eq2: diff(L(x,y,lambda),y)=0; eq3: diff(L(x,y,lambda),lambda)=0; sol: solve([eq1,eq2,eq3], [x,y,lambda]);
Η λύση που λαμβάνεται είναι:
$$ [x=6,y=8,lambda=\frac{1}{5}]] $$
Μπορούμε να κρατήσουμε τη λύση στις μεταβλητές x0,y0:
x0 : rhs(sol[1][1]); y0 : rhs(sol[1][2]);
Και να βρούμε το επίπεδο μέγιστης χρησιμότητας:
U0 : U(x0,y0);
Το οποίο είναι 10
Ή, να υπολογίσουμε για επιβεβαίωση την κατανάλωση:
C(x,y) := x*Px + y*Py; C0 : C(x0,y0);
Η οποία είναι 50.
Για το δεύτερο μέρος της άσκησης μπορείτε επίσης να συμβουλευτείτε τη σελίδα.
Για να κάνουμε το γράφημα της καμπύλης αδιαφορίας, χρειάζεται να λύσουμε τη συνάρτηση χρησιμότητας $$U(x,y)=U0$$ ως προς y:
sol: solve([U(x,y) = U0], y);
με αποτέλεσμα:
$$[y=-\sqrt{100-{x}^{2}},y=\sqrt{100-{x}^{2}}]$$
Θα πρέπει να ορίσουμε μια νέα συνάρτηση με το θετικό μέρος της καμπύλης:
f(x) := sqrt(100-x^2);
και στη συνέχεια να ορίσουμε τη συνάρτηση της παραγώγου και την ευθεία που η παράγωγος τέμνει τη καμπύλη αδιαφορίας στο x0:
g(x) := ''(diff(f(x), x)); h(x) := ''(g(x0)*x+f(x0)-x0*g(x0));
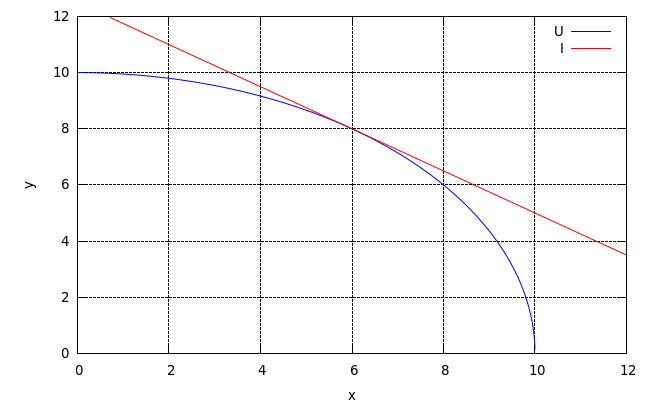
Τέλος, το γράφημα είναι, πιστεύω, απλή υπόθεση:
plot2d([f(x),h(x)], [x,0,12], [y,0,12], [legend, "U","I"]);
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.