Κατανομή του εκτιμητή OLS με προσομοίωση monte carlo στο Octave/Matlab
Έστω το γραμμικό μοντέλο:
$$ y = X \beta + u $$
όπου Χ είναι διάνυσμα T θέσεων (παρατηρήσεων).
Ποια είναι η κατανομή του εκτιμητή OLS:
$$ \hat{\beta} = (X'X)^{-1}X'y $$
Υποθέτουμε πως τόσο τα κατάλοιπα όσο και η ερμηνευτική μεταβλητή κατανέμονται κανονικά.
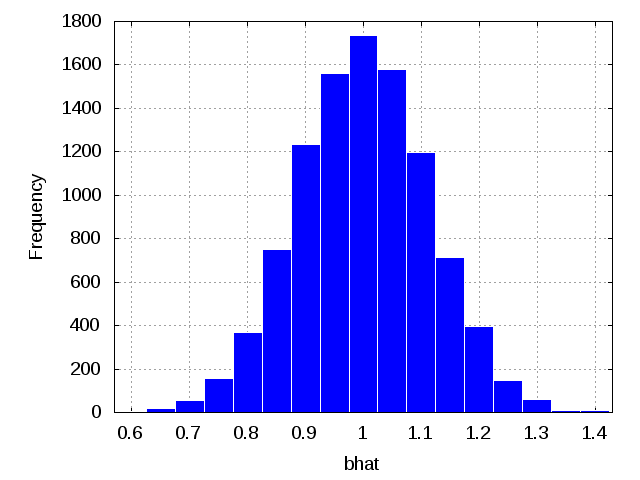
Το πρόγραμμα (script) σε Octave/Μatlab για τον υπολογισμό και την κατασκευή του ιστογράμματος (υποθέτουμε β=1):
clear;
T = 100;
N = 10000;
x = normrnd(0, 1, T, 1);
bhat = [];
for (i = 1:N)
u = normrnd(0, 1, T, 1);
y = x + u;
bhat(i) = (x'*x)^-1 * x'*y;
end
hist(bhat, 0.6:0.05:1.4, 'Facecolor', 'b', 'Edgecolor', 'w')
xlabel('bhat');
ylabel('Frequency');
grid on;
Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.