Άθροισμα σειράς, εκτίμηση π με τη μέθοδο Leibnitz

Η μέθοδος στηρίζεται στον τύπο:

$$ \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \sum_{n=0}^\infty \frac{(-1)^n}{2n+1} $$

Ο υπολογισμός στο maxima μπορεί να γίνει ως εξής:

K   : 100;
ser : (-1)^n/(2*n+1);
pi4 : nusum(ser, n, 0, K), numer;
4*pi4;

Όπως δείχνει και το παρακάτω σχήμα:

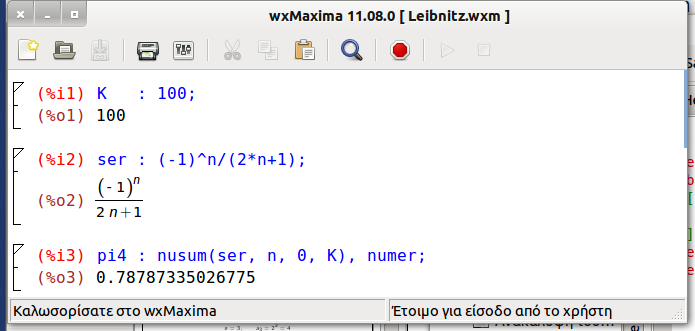
leibnitz

Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον Αθανάσιο Σταυρακούδη σας παρέχετε κάτω από την άδεια Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.