Υπολογισμός ελάχιστου συνάρτησης δύο μεταβλητών με τυχαία αναζήτηση στο Octave/Matlab
Έστω η συνάρτηση:
$$ f(x_1, x_2) = x_1^2 + x_2^2 $$
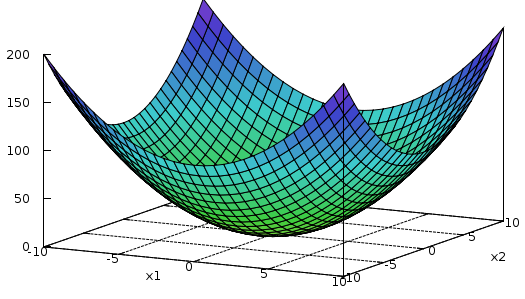
Να βρεθεί το ελάχιστο της συνάρτησης με τη μέθοδο της τυχαίας αναζήτησης
- Δίνουμε T αρχικές τιμές στο x με εύρος τιμών ±L
- Βρίσκουμε τη μικρότερη τιμή του y και τις αντίστοιχες τιμές του x
- Μειώνουμε το εύρος L στο μισό
- Επαναλαμβάνουμε τη διαδικασία έως ότου η απόλυτη διαφορά δύο διαδοχικών ελάχιστων y είναι μικρότερη από μια επιθυμητή ακρίβεια
# Βελτιστοποίηση συνάρτησης δύο μεταβλητών με τυχαία αναζήτηση
# Βασικό Octave script των υπολογισμών
# Αθανάσιος Σταυρακούδης
# http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=472
# 17 Δεκεμβρίου 2012
clear;
# Συνάρτηση προς ελαχιστοποίηση
function y = f(x1, x2)
y = x1 .^ 2 + x2 .^ 2;
end
T = 1E+4; # Πλήθος σημείων
N = 1E+2; # Μέγιστο πλήθος επαναλήψεων
L = 1E+2; # Αρχικό εύρος (x-L, x+L)
h = 1E-6; # Ακρίβεια της μεθόδου
# Αρχικοποίηση της μεθόδου
x1 = unifrnd(-L, L, T, 1);
x2 = unifrnd(-L, L, T, 1);
y = f(x1, x2);
[v k] = min(y);
fval(1) = y(k);
mx1(1) = x1(k);
mx2(1) = x2(k);
printf ("\n");
printf ("Ελαχιστοποίηση συνάρτησης με τυχαία αναζήτηση\n\n");
# Επανάληψη της διαδικασίας με σταδιακή μείωση τους εύρους L
i = 2;
while (i <= N)
L = L / 2;
x1 = unifrnd(x1(k)-L, x1(k)+L, T, 1);
x2 = unifrnd(x2(k)-L, x2(k)+L, T, 1);
y = f(x1, x2);
[v k] = min(y);
fval(i) = y(k);
mx1(i) = x1(k);
mx2(i) = x2(k);
dfval = fval(i) - fval(i-1);
dx1 = mx1(i) - mx2(i-1);
dx2 = mx2(i) - mx1(i-1);
if ( abs(dfval) < h )
break;
end
i++;
end
# Αποτελέσματα
printf ("Τέλος της διαδικασίας μετά από %d επαναλήψεις\n\n", i);
printf ("Το ελάχιστο που βρέθηκε: y = %16.12f\n", fval(i));
printf (" x1 = %16.12f\n", mx1(i));
printf (" x2 = %16.12f\n", mx2(i));
Δοκιμάστε τη μέθοδο με άλλη συνάρτηση. Δοκιμάστε την αποτελεσματικότητα της μεθόδου αλλάζοντας τις τιμές των T, N, L.
Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.