Η μέθοδος Euler για την επίλυση διαφορικής εξίσωσης με το Octave/Matlab
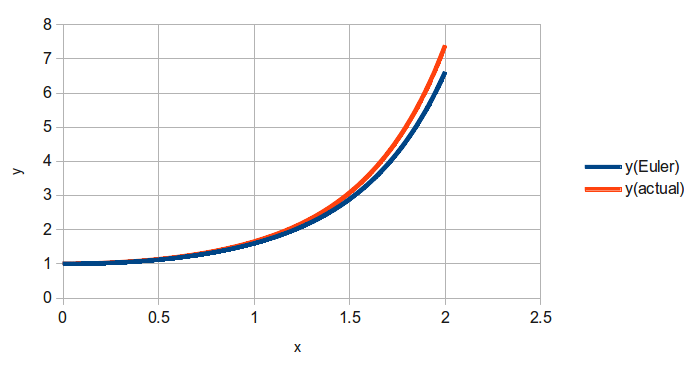
Έστω η διαφορική εξίσωση:
$$ \frac{dy}{dx} = xy $$
με αρχικές συνθήκες
$$ x_0 = 0, \quad y_0 =1 $$
Δείτε την περιγραφή της μεθόδου εδώ: Η μέθοδος Euler για την επίλυση διαφορικής εξίσωσης με το Excel/Calc
Στην ουσία, χρειαζόμαστε ένα πίνακα τιμών της συνάρτησης.
clear; delta = 0.05; N = 10; x = zeros(N+1,1); y = zeros(N+1,1); i = 1; x(1) = 0; y(1) = 1; for (i = 2:N+1) x(i) = x(i-1) + delta; y(i) = y(i-1) + delta * x(i-1) * y(i-1); end [x y]
Παράδειγμα εκτέλεσης:
octave:> euler1 ans = 0.00000 1.00000 0.05000 1.00000 0.10000 1.00250 0.15000 1.00751 0.20000 1.01507 0.25000 1.02522 0.30000 1.03803 0.35000 1.05361 0.40000 1.07204 0.45000 1.09348 0.50000 1.11809
Συνδεθείτε για περισσότερες δυνατότητες αλληλεπίδρασης,
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.
σχολιασμοί, εξωτερικοί σύνδεσμοι, βοήθεια, ψηφοφορίες, αρχεία, κτλ.

Εκπαιδευτικό υλικό από τον
Αθανάσιο Σταυρακούδη
σας παρέχετε κάτω από την άδεια
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 License.
Σας παρακαλώ να ενημερωθείτε για κάποιους επιπλέον περιορισμούς
http://stavrakoudis.econ.uoi.gr/stavrakoudis/?iid=401.